Uncertainty II

POL51

Juan Tellez

jftellez@ucdavis.edu

UC Davis

November 27, 2024

Plan for today

Quantifying uncertainty

The confidence interval

Are we sure it’s not zero?

Where are we at?

The problem

We know our analysis is based on samples, and different samples give different answers:

Average number of kids in samples of size 10
Sample	Avg. num of kids in sample
1	1.4
2	2.4
3	1.5
4	2.1
5	1.5
6	2.0
7	1.2
8	2.0

The way out

Turns out that if our samples are representative of the population, then estimates from large samples will tend to be pretty damn close
So if sample is good ✅ and “big” ✅ then most of the time we’ll be OK ✅

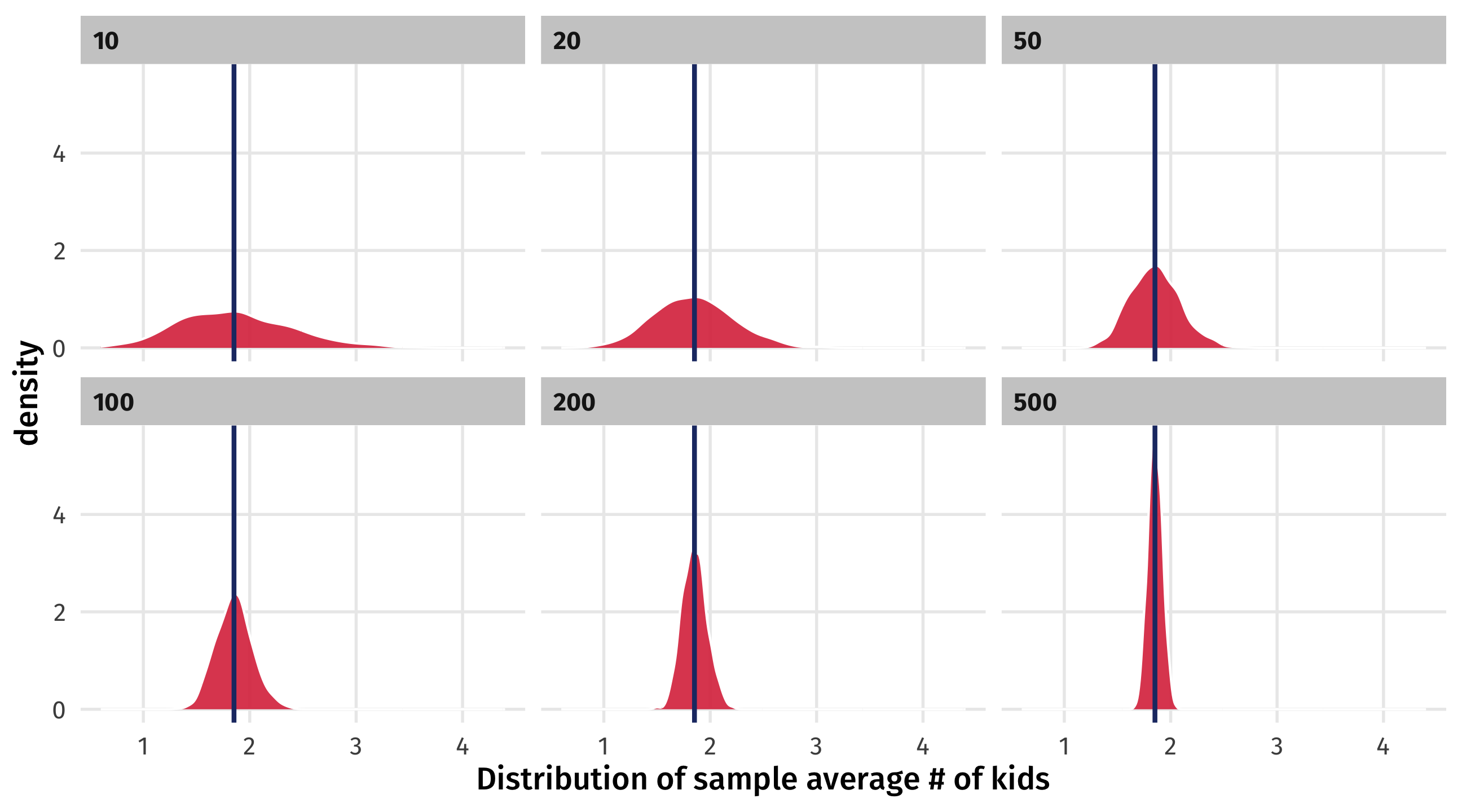
But this is weird

We’ve shown that if we take many (large) random samples, most of the averages of those samples will be close to population parameter

But in real life we only ever have one sample (e.g., one poll)

How do we get a sense for uncertainty from our one sample?

Two approaches

❌ ~~Statistical theory~~

Make assumptions about distribution of samples from population
Design test based on those assumptions (t-test, z-test, etc.)

✅ Simulation

Simulate different samples that look like ours
Use distribution of simulated samples to quantify uncertainty

In some cases, both get you to the same answer, in others, only one works

Simulation

We want a sense for how uncertain we should feel on estimates drawn from our sample

Our sample is gss_sm, and we have 2,867 observations

gss_sm
year	id	ballot	age	childs	sibs	degree	race
2016	2830	2	62	2	2	Bachelor	White
2016	848	3	28	1	3	High School	Black
2016	2186	2	32	0	1	High School	White
2016	198	1	49	0	4	Bachelor	Other
2016	985	1	50	1	1	High School	White

How confident are we in the estimate we get from this sample, given its size?

How to simulate

If we take lots of samples of size 20 \(\rightarrow\) uncertainty in a sample of 20

gss_sm %>%
  rep_sample_n(size = 20, reps = 1000)

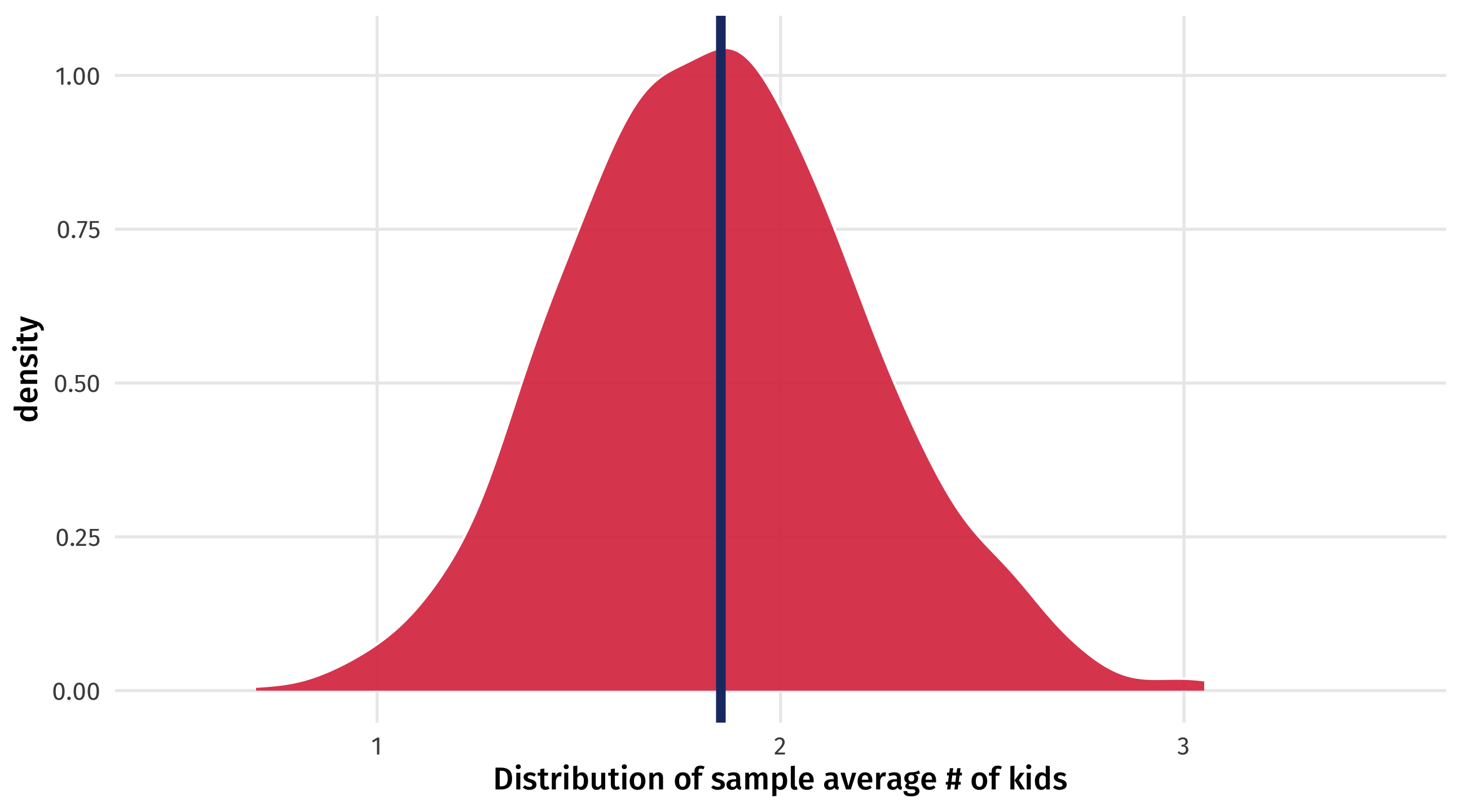
How to simulate

If we take lots of samples of size 100 \(\rightarrow\) uncertainty in a sample of 100

gss_sm %>%
  rep_sample_n(size = 100, reps = 1000)

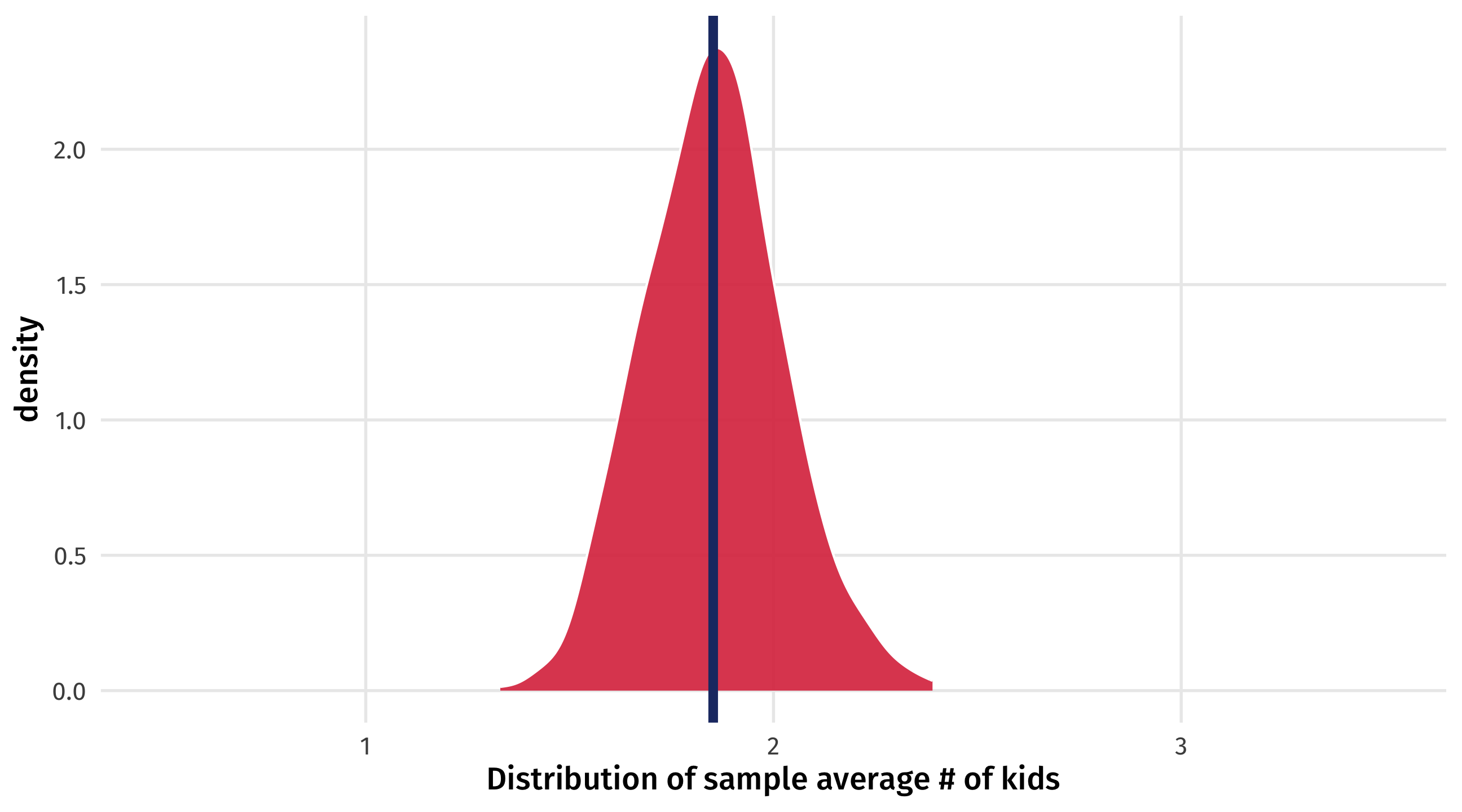
How to simulate

So to see how uncertain we should feel about gss_sm, we should take many samples that are the same size as gss_sm

gss_sm %>% 
  rep_sample_n(size = 2867, reps = 1000)

gss_sm %>% 
  rep_sample_n(size = nrow(gss_sm), reps = 1000)

Note

nrow(DATA) tells you how many observations in data object

Problem

If we have a dataset of 2,867 observations and ask R to randomly pick 2,867 observations, we’ll just get a bunch of copies of the original dataset

gss_sm %>% 
  rep_sample_n(size = nrow(gss_sm), reps = 1000)

Solution: sample with replacement \(\rightarrow\) once we draw an observation it goes back into the dataset, and can be sampled again

gss_sm %>% 
  rep_sample_n(size = nrow(gss_sm), reps = 1000, replace = TRUE)

Note

replace = TRUE allows an observation to be re-sampled

Sampling with replacement

Sampling with and without replacement

If we were sampling 4 of these delicious fruits:

Dataset on fruits
fruits
Mango
Pineapple
Banana
Blackberry

Sampling with and without replacement

Without replacement:

rep_sample_n(food, size = 4, reps = 1)

# A tibble: 4 × 2
# Groups:   replicate [1]
  replicate fruits    
      <int> <chr>     
1         1 Mango     
2         1 Pineapple 
3         1 Blackberry
4         1 Banana

With replacement:

rep_sample_n(food, size = 4, reps = 1, replace = TRUE)

# A tibble: 4 × 2
# Groups:   replicate [1]
  replicate fruits    
      <int> <chr>     
1         1 Blackberry
2         1 Banana    
3         1 Banana    
4         1 Banana

Bootstrapping

Generating many, same-sized samples with replacement is called bootstrapping
Replacement lets us generate samples that randomly differ from ours
Use the distribution of bootstrapped samples to quantify uncertainty

Only one sample? Pull yourself up by your bootstraps!

Back to the kids

How uncertain should we be of our estimate of the avg. number of kids in the US, Given that it’s based on our one sample, gss_sm? We can bootstrap:

boot_kids = gss_sm %>% 
  rep_sample_n(size = nrow(gss_sm), reps = 1000, replace = TRUE) %>% 
  summarise(avg_kids = mean(childs, na.rm = TRUE))
boot_kids

replicate	avg_kids
1	1.89
2	1.84
3	1.82
4	1.79
5	1.84
6	1.9
7	1.9
8	1.83
9	1.83
10	1.88
11	1.89
12	1.88
13	1.84
14	1.78
15	1.79
16	1.84
17	1.83
18	1.88
19	1.8
20	1.82
21	1.86
22	1.85
23	1.82
24	1.85
25	1.9
26	1.86
27	1.84
28	1.95
29	1.85
30	1.89
31	1.89
32	1.82
33	1.83
34	1.83
35	1.84
36	1.81
37	1.88
38	1.81
39	1.84
40	1.84
41	1.86
42	1.92
43	1.86
44	1.8
45	1.86
46	1.85
47	1.91
48	1.85
49	1.86
50	1.92
51	1.82
52	1.81
53	1.93
54	1.78
55	1.84
56	1.8
57	1.79
58	1.88
59	1.85
60	1.83
61	1.85
62	1.84
63	1.88
64	1.78
65	1.87
66	1.83
67	1.88
68	1.86
69	1.83
70	1.84
71	1.9
72	1.85
73	1.83
74	1.84
75	1.84
76	1.88
77	1.79
78	1.82
79	1.85
80	1.88
81	1.82
82	1.83
83	1.77
84	1.91
85	1.9
86	1.86
87	1.9
88	1.83
89	1.84
90	1.91
91	1.85
92	1.81
93	1.84
94	1.88
95	1.89
96	1.86
97	1.87
98	1.82
99	1.83
100	1.82
101	1.88
102	1.83
103	1.76
104	1.84
105	1.84
106	1.8
107	1.87
108	1.86
109	1.86
110	1.86
111	1.84
112	1.85
113	1.87
114	1.86
115	1.87
116	1.86
117	1.87
118	1.89
119	1.82
120	1.82
121	1.89
122	1.9
123	1.86
124	1.85
125	1.89
126	1.83
127	1.85
128	1.8
129	1.83
130	1.87
131	1.81
132	1.87
133	1.83
134	1.81
135	1.88
136	1.86
137	1.88
138	1.82
139	1.82
140	1.85
141	1.83
142	1.84
143	1.85
144	1.78
145	1.83
146	1.93
147	1.9
148	1.83
149	1.84
150	1.91
151	1.84
152	1.79
153	1.83
154	1.83
155	1.83
156	1.85
157	1.86
158	1.86
159	1.84
160	1.82
161	1.88
162	1.76
163	1.9
164	1.87
165	1.88
166	1.89
167	1.84
168	1.88
169	1.9
170	1.85
171	1.88
172	1.83
173	1.81
174	1.84
175	1.86
176	1.8
177	1.83
178	1.86
179	1.87
180	1.82
181	1.87
182	1.85
183	1.91
184	1.81
185	1.83
186	1.83
187	1.84
188	1.88
189	1.84
190	1.83
191	1.85
192	1.88
193	1.87
194	1.84
195	1.84
196	1.83
197	1.9
198	1.78
199	1.86
200	1.81
201	1.89
202	1.85
203	1.88
204	1.85
205	1.81
206	1.87
207	1.84
208	1.81
209	1.86
210	1.85
211	1.8
212	1.8
213	1.86
214	1.88
215	1.86
216	1.86
217	1.87
218	1.86
219	1.79
220	1.89
221	1.88
222	1.85
223	1.84
224	1.81
225	1.81
226	1.8
227	1.84
228	1.9
229	1.95
230	1.86
231	1.83
232	1.84
233	1.84
234	1.84
235	1.84
236	1.87
237	1.86
238	1.84
239	1.88
240	1.91
241	1.81
242	1.87
243	1.79
244	1.86
245	1.82
246	1.83
247	1.89
248	1.85
249	1.92
250	1.84
251	1.9
252	1.9
253	1.8
254	1.91
255	1.9
256	1.83
257	1.86
258	1.82
259	1.84
260	1.86
261	1.88
262	1.83
263	1.83
264	1.86
265	1.84
266	1.87
267	1.83
268	1.87
269	1.84
270	1.85
271	1.85
272	1.84
273	1.83
274	1.87
275	1.83
276	1.86
277	1.87
278	1.87
279	1.86
280	1.87
281	1.83
282	1.83
283	1.92
284	1.9
285	1.88
286	1.79
287	1.84
288	1.87
289	1.83
290	1.9
291	1.82
292	1.84
293	1.87
294	1.88
295	1.86
296	1.85
297	1.84
298	1.84
299	1.8
300	1.86
301	1.91
302	1.87
303	1.83
304	1.86
305	1.81
306	1.86
307	1.79
308	1.89
309	1.8
310	1.91
311	1.91
312	1.86
313	1.89
314	1.82
315	1.82
316	1.88
317	1.83
318	1.86
319	1.8
320	1.87
321	1.83
322	1.88
323	1.87
324	1.82
325	1.81
326	1.87
327	1.81
328	1.93
329	1.85
330	1.84
331	1.85
332	1.81
333	1.89
334	1.81
335	1.87
336	1.88
337	1.85
338	1.86
339	1.84
340	1.86
341	1.82
342	1.85
343	1.85
344	1.83
345	1.89
346	1.85
347	1.85
348	1.87
349	1.88
350	1.82
351	1.86
352	1.88
353	1.87
354	1.84
355	1.85
356	1.86
357	1.86
358	1.79
359	1.88
360	1.89
361	1.92
362	1.81
363	1.86
364	1.84
365	1.89
366	1.9
367	1.83
368	1.84
369	1.87
370	1.9
371	1.88
372	1.85
373	1.88
374	1.87
375	1.86
376	1.79
377	1.91
378	1.82
379	1.84
380	1.88
381	1.84
382	1.82
383	1.89
384	1.85
385	1.84
386	1.83
387	1.86
388	1.83
389	1.87
390	1.85
391	1.86
392	1.86
393	1.83
394	1.85
395	1.81
396	1.86
397	1.86
398	1.79
399	1.82
400	1.86
401	1.86
402	1.82
403	1.81
404	1.85
405	1.8
406	1.89
407	1.87
408	1.89
409	1.81
410	1.85
411	1.87
412	1.83
413	1.92
414	1.89
415	1.87
416	1.85
417	1.81
418	1.86
419	1.91
420	1.88
421	1.79
422	1.87
423	1.86
424	1.85
425	1.89
426	1.88
427	1.83
428	1.84
429	1.9
430	1.82
431	1.87
432	1.89
433	1.87
434	1.87
435	1.89
436	1.86
437	1.93
438	1.85
439	1.86
440	1.85
441	1.84
442	1.87
443	1.81
444	1.84
445	1.86
446	1.92
447	1.82
448	1.89
449	1.82
450	1.85
451	1.83
452	1.89
453	1.86
454	1.8
455	1.85
456	1.87
457	1.81
458	1.87
459	1.85
460	1.82
461	1.85
462	1.84
463	1.89
464	1.85
465	1.87
466	1.88
467	1.86
468	1.82
469	1.9
470	1.9
471	1.85
472	1.84
473	1.82
474	1.83
475	1.84
476	1.81
477	1.83
478	1.82
479	1.83
480	1.86
481	1.84
482	1.83
483	1.84
484	1.82
485	1.88
486	1.85
487	1.8
488	1.86
489	1.84
490	1.84
491	1.86
492	1.87
493	1.8
494	1.84
495	1.86
496	1.88
497	1.83
498	1.84
499	1.89
500	1.83
501	1.87
502	1.84
503	1.88
504	1.84
505	1.84
506	1.83
507	1.85
508	1.87
509	1.86
510	1.81
511	1.84
512	1.87
513	1.88
514	1.82
515	1.84
516	1.83
517	1.85
518	1.81
519	1.87
520	1.86
521	1.84
522	1.87
523	1.87
524	1.84
525	1.83
526	1.83
527	1.91
528	1.78
529	1.88
530	1.9
531	1.8
532	1.81
533	1.83
534	1.81
535	1.81
536	1.79
537	1.89
538	1.8
539	1.85
540	1.82
541	1.9
542	1.92
543	1.85
544	1.84
545	1.86
546	1.82
547	1.87
548	1.81
549	1.86
550	1.87
551	1.83
552	1.82
553	1.83
554	1.92
555	1.82
556	1.79
557	1.84
558	1.8
559	1.84
560	1.85
561	1.84
562	1.81
563	1.85
564	1.85
565	1.82
566	1.86
567	1.83
568	1.86
569	1.83
570	1.85
571	1.88
572	1.85
573	1.88
574	1.81
575	1.82
576	1.79
577	1.84
578	1.8
579	1.89
580	1.84
581	1.88
582	1.84
583	1.83
584	1.84
585	1.85
586	1.86
587	1.85
588	1.82
589	1.88
590	1.83
591	1.83
592	1.88
593	1.8
594	1.81
595	1.82
596	1.84
597	1.86
598	1.87
599	1.87
600	1.9
601	1.78
602	1.84
603	1.81
604	1.89
605	1.83
606	1.85
607	1.86
608	1.83
609	1.81
610	1.87
611	1.87
612	1.87
613	1.85
614	1.86
615	1.89
616	1.84
617	1.8
618	1.81
619	1.83
620	1.82
621	1.85
622	1.78
623	1.82
624	1.89
625	1.9
626	1.83
627	1.8
628	1.89
629	1.85
630	1.88
631	1.88
632	1.84
633	1.83
634	1.84
635	1.87
636	1.84
637	1.85
638	1.82
639	1.85
640	1.91
641	1.86
642	1.82
643	1.86
644	1.78
645	1.85
646	1.84
647	1.85
648	1.9
649	1.84
650	1.84
651	1.84
652	1.85
653	1.9
654	1.81
655	1.86
656	1.83
657	1.79
658	1.87
659	1.91
660	1.89
661	1.91
662	1.87
663	1.85
664	1.83
665	1.83
666	1.86
667	1.85
668	1.86
669	1.86
670	1.87
671	1.82
672	1.84
673	1.84
674	1.83
675	1.87
676	1.84
677	1.88
678	1.8
679	1.86
680	1.86
681	1.85
682	1.9
683	1.86
684	1.82
685	1.8
686	1.83
687	1.86
688	1.82
689	1.83
690	1.89
691	1.82
692	1.83
693	1.81
694	1.82
695	1.87
696	1.91
697	1.88
698	1.87
699	1.87
700	1.89
701	1.84
702	1.84
703	1.84
704	1.83
705	1.82
706	1.81
707	1.85
708	1.83
709	1.87
710	1.84
711	1.82
712	1.89
713	1.83
714	1.85
715	1.84
716	1.89
717	1.83
718	1.79
719	1.86
720	1.84
721	1.84
722	1.84
723	1.87
724	1.85
725	1.84
726	1.89
727	1.86
728	1.86
729	1.86
730	1.83
731	1.79
732	1.87
733	1.81
734	1.87
735	1.86
736	1.88
737	1.85
738	1.84
739	1.88
740	1.85
741	1.88
742	1.84
743	1.82
744	1.78
745	1.8
746	1.87
747	1.83
748	1.8
749	1.84
750	1.79
751	1.84
752	1.86
753	1.87
754	1.92
755	1.86
756	1.86
757	1.88
758	1.85
759	1.87
760	1.77
761	1.79
762	1.83
763	1.88
764	1.85
765	1.84
766	1.83
767	1.83
768	1.87
769	1.8
770	1.84
771	1.88
772	1.85
773	1.91
774	1.89
775	1.86
776	1.82
777	1.81
778	1.87
779	1.85
780	1.83
781	1.88
782	1.8
783	1.81
784	1.82
785	1.89
786	1.88
787	1.86
788	1.81
789	1.84
790	1.87
791	1.84
792	1.84
793	1.86
794	1.87
795	1.91
796	1.9
797	1.85
798	1.86
799	1.84
800	1.9
801	1.79
802	1.89
803	1.81
804	1.8
805	1.83
806	1.78
807	1.84
808	1.87
809	1.81
810	1.86
811	1.88
812	1.82
813	1.84
814	1.79
815	1.87
816	1.81
817	1.88
818	1.8
819	1.86
820	1.9
821	1.87
822	1.87
823	1.85
824	1.85
825	1.88
826	1.91
827	1.84
828	1.86
829	1.89
830	1.85
831	1.84
832	1.79
833	1.83
834	1.86
835	1.83
836	1.83
837	1.87
838	1.88
839	1.86
840	1.84
841	1.87
842	1.87
843	1.84
844	1.84
845	1.89
846	1.88
847	1.82
848	1.83
849	1.89
850	1.85
851	1.8
852	1.85
853	1.84
854	1.91
855	1.87
856	1.86
857	1.82
858	1.87
859	1.87
860	1.87
861	1.81
862	1.91
863	1.84
864	1.93
865	1.87
866	1.8
867	1.84
868	1.88
869	1.85
870	1.84
871	1.9
872	1.87
873	1.84
874	1.83
875	1.88
876	1.85
877	1.88
878	1.9
879	1.82
880	1.86
881	1.8
882	1.89
883	1.91
884	1.94
885	1.83
886	1.93
887	1.84
888	1.83
889	1.86
890	1.85
891	1.87
892	1.88
893	1.83
894	1.82
895	1.82
896	1.79
897	1.88
898	1.84
899	1.79
900	1.87
901	1.87
902	1.89
903	1.85
904	1.85
905	1.84
906	1.94
907	1.89
908	1.86
909	1.85
910	1.89
911	1.85
912	1.76
913	1.86
914	1.91
915	1.84
916	1.94
917	1.88
918	1.82
919	1.89
920	1.8
921	1.82
922	1.86
923	1.86
924	1.88
925	1.83
926	1.86
927	1.85
928	1.82
929	1.84
930	1.89
931	1.81
932	1.86
933	1.83
934	1.83
935	1.9
936	1.85
937	1.85
938	1.87
939	1.84
940	1.85
941	1.83
942	1.88
943	1.91
944	1.83
945	1.82
946	1.84
947	1.87
948	1.88
949	1.9
950	1.88
951	1.85
952	1.79
953	1.84
954	1.87
955	1.83
956	1.87
957	1.88
958	1.86
959	1.83
960	1.87
961	1.86
962	1.82
963	1.84
964	1.85
965	1.87
966	1.84
967	1.84
968	1.86
969	1.81
970	1.87
971	1.83
972	1.83
973	1.9
974	1.85
975	1.83
976	1.88
977	1.86
978	1.86
979	1.88
980	1.85
981	1.83
982	1.84
983	1.86
984	1.87
985	1.82
986	1.84
987	1.77
988	1.84
989	1.87
990	1.82
991	1.87
992	1.88
993	1.84
994	1.81
995	1.84
996	1.84
997	1.82
998	1.79
999	1.85
1000	1.83

The distribution of bootstrapped estimates

Our estimate and how much simulated estimates might vary across bootstrapped samples that look like ours

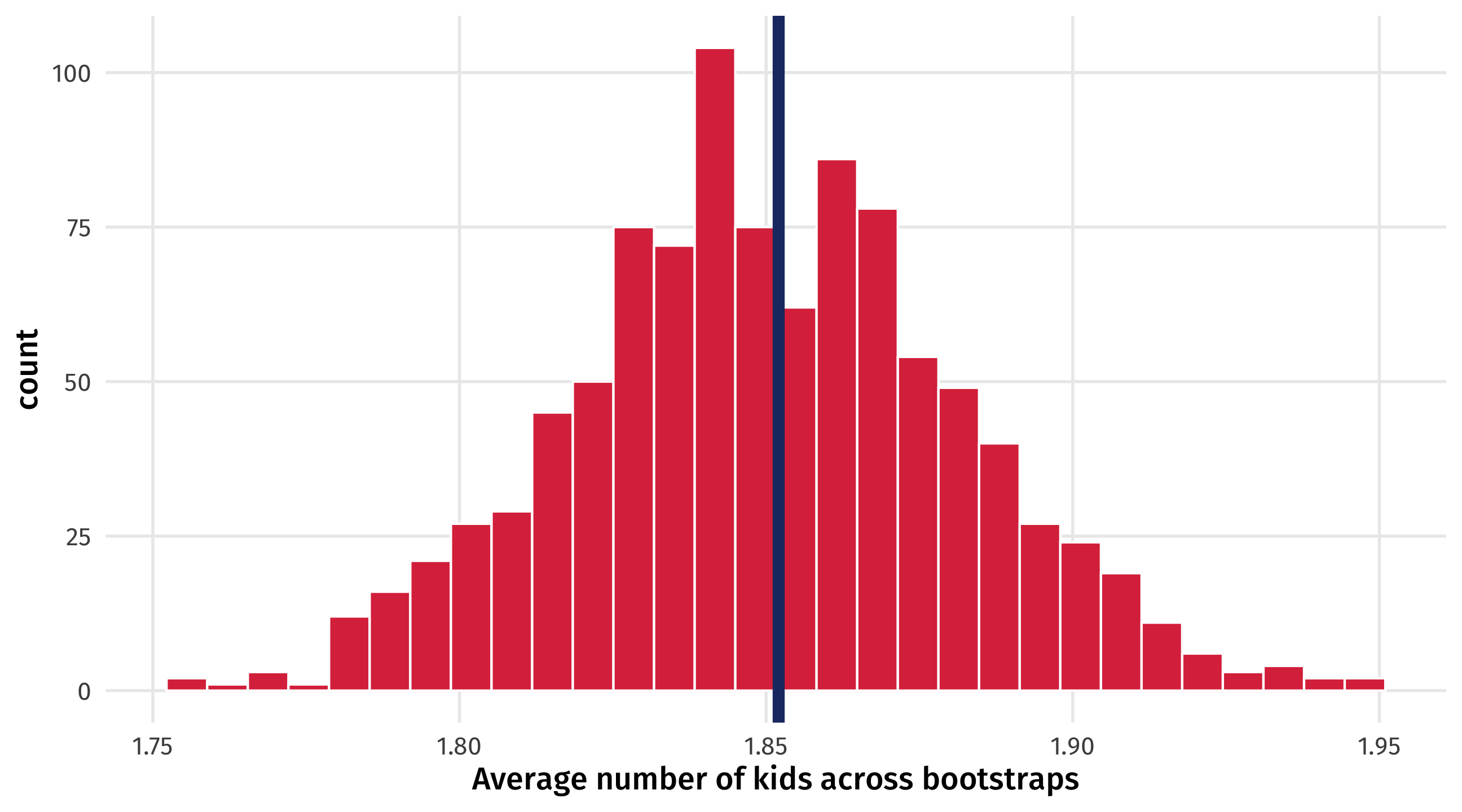
The red is the distribution of bootstrapped sample estimates \(\rightarrow\) the sampling distribution

Your turn: Income and household assets

wealth is all dummy variables, tell you whether household in Honduras 🇭🇳 has a particular asset or not:

Sample from `wealth`
r1	r3	r4a	r7	r8	r12	r14	r15	r16	r18	ur	ed	q10new_18	q14	fs2	fs8
1	1	1	0	1	1	1	0	0	0	Urban	7	2	0	0	0
1	1	1	1	0	1	1	0	0	0	Rural	3	NA	0	0	0
1	1	1	0	0	1	0	1	0	1	Rural	6	1	0	0	0
1	1	1	0	0	0	0	0	0	0	Rural	2	1	1	0	0
0	0	1	0	0	1	1	0	NA	0	Urban	2	6	0	1	1

Your turn: Income and household assets

Using wealth from juanr, pick an asset from the codebook:

What percent of households own that asset?
How uncertain should you be of your estimate? Generate 1,000 bootstraps and plot the distribution.

10:00

Quantifying uncertainty

How to quantify uncertainty?

The red histogram is nice, but how can we communicate uncertainty in our estimates in a pithy, more comparable way?

Three approaches:

The standard error
The confidence interval
Statistical significance

The standard error

One way to quantify uncertainty would be to measure how “wide” the distribution of bootstrapped sample estimates is

As we learned so long ago, one way to measure the “spread” of a distribution (i.e., how much a variable varies), is with the standard deviation

The standard deviation of the sampling distribution is called the standard error, or the margin of error

The standard error

Generate bootstraps:

boot_kids = gss_sm %>% 
  rep_sample_n(size = nrow(gss_sm), reps = 1000, replace = TRUE) %>% 
  summarise(avg_kids = mean(childs, na.rm = TRUE))

Calculate the mean and standard error of the bootstraps:

boot_kids %>% 
  summarise(mean = mean(avg_kids), standard_error = sd(avg_kids))

mean	standard_error
1.85	0.0303

Best guess? About 1.85 kids, +/- 2 standard errors (1.85 - 2 * .03 = 1.79, 1.85 + 2 * .03 = 1.91)

Standard error

This is what you see in the news – that +/- polling/margin of error

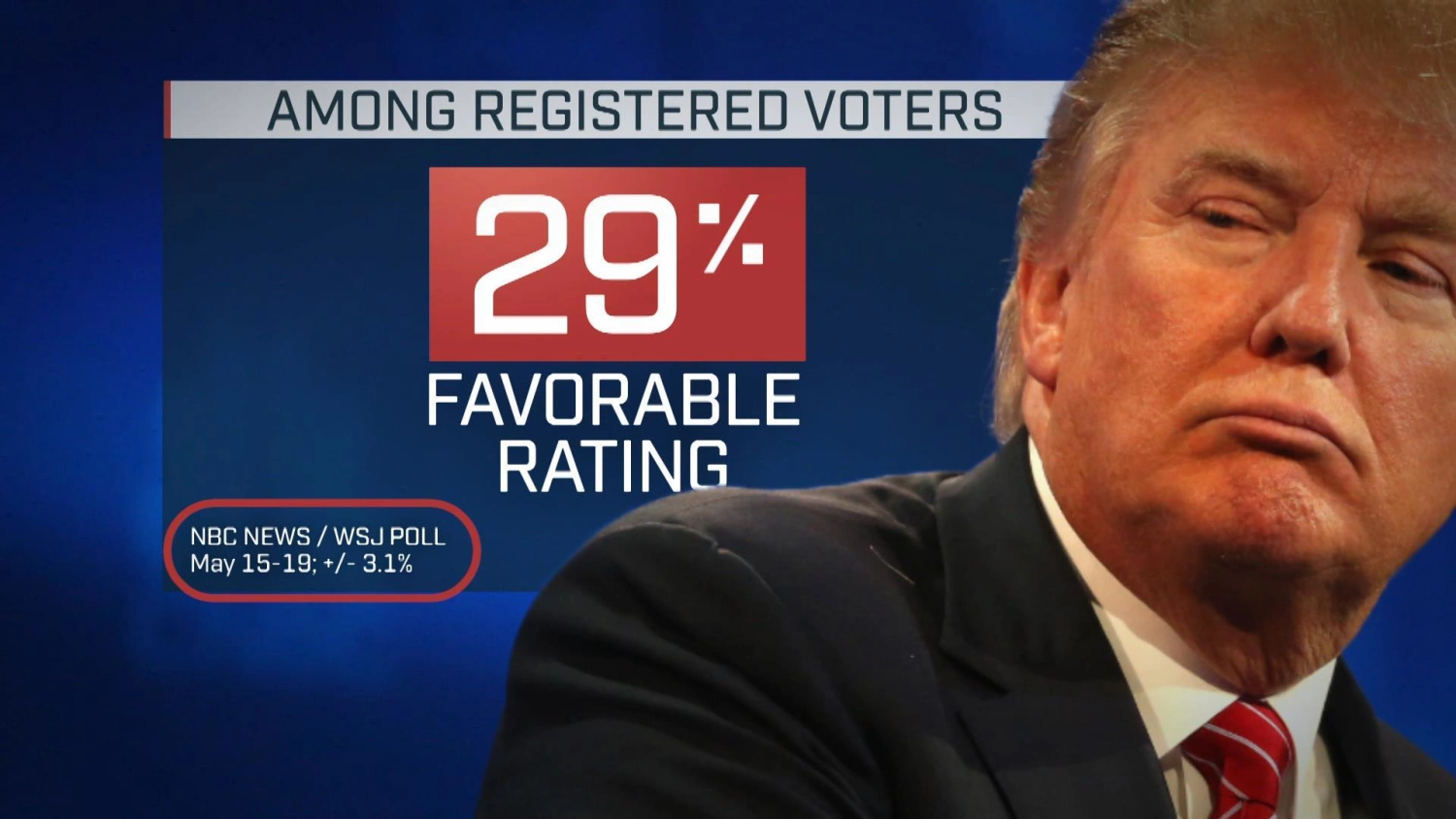
Varying uncertainty

Standard errors get smaller as sample sizes get larger:

Sample size	Average (truth = 10)	Standard error
10	10.28	0.46
64	10.23	0.25
119	9.82	0.20
173	9.94	0.15
228	9.97	0.12
282	10.15	0.12
337	10.11	0.12
391	10.16	0.10
446	10.06	0.10
500	9.93	0.09

The confidence interval

Another way to quantify uncertainty is to look where most estimates fall

this is the confidence interval: our “best guess” of what we’re trying to estimate

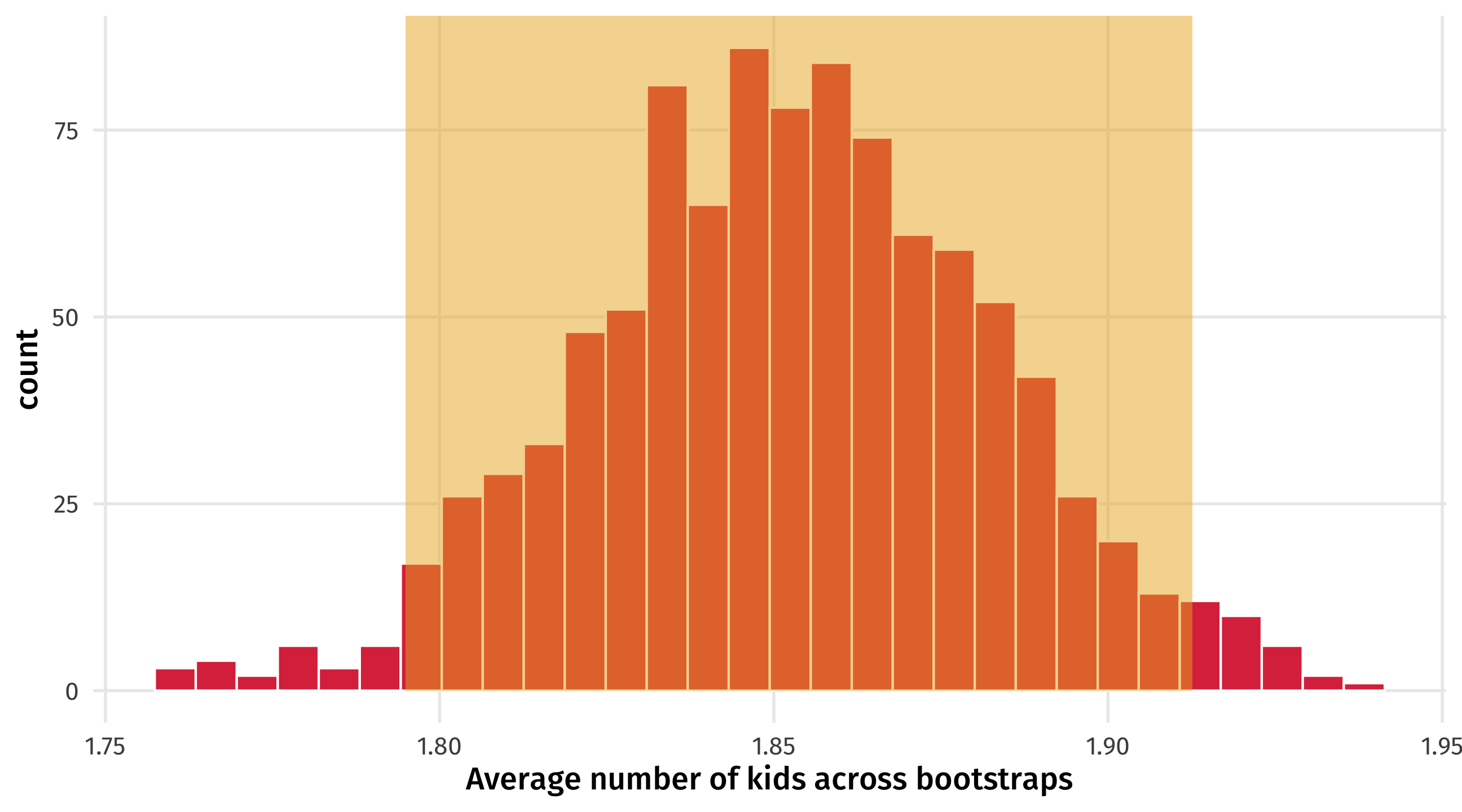
How big to make the interval?

You could report (for example) where the middle 50% of bootstraps fall, or (for example) where the middle 95% of bootstraps fall, but there are tradeoffs!

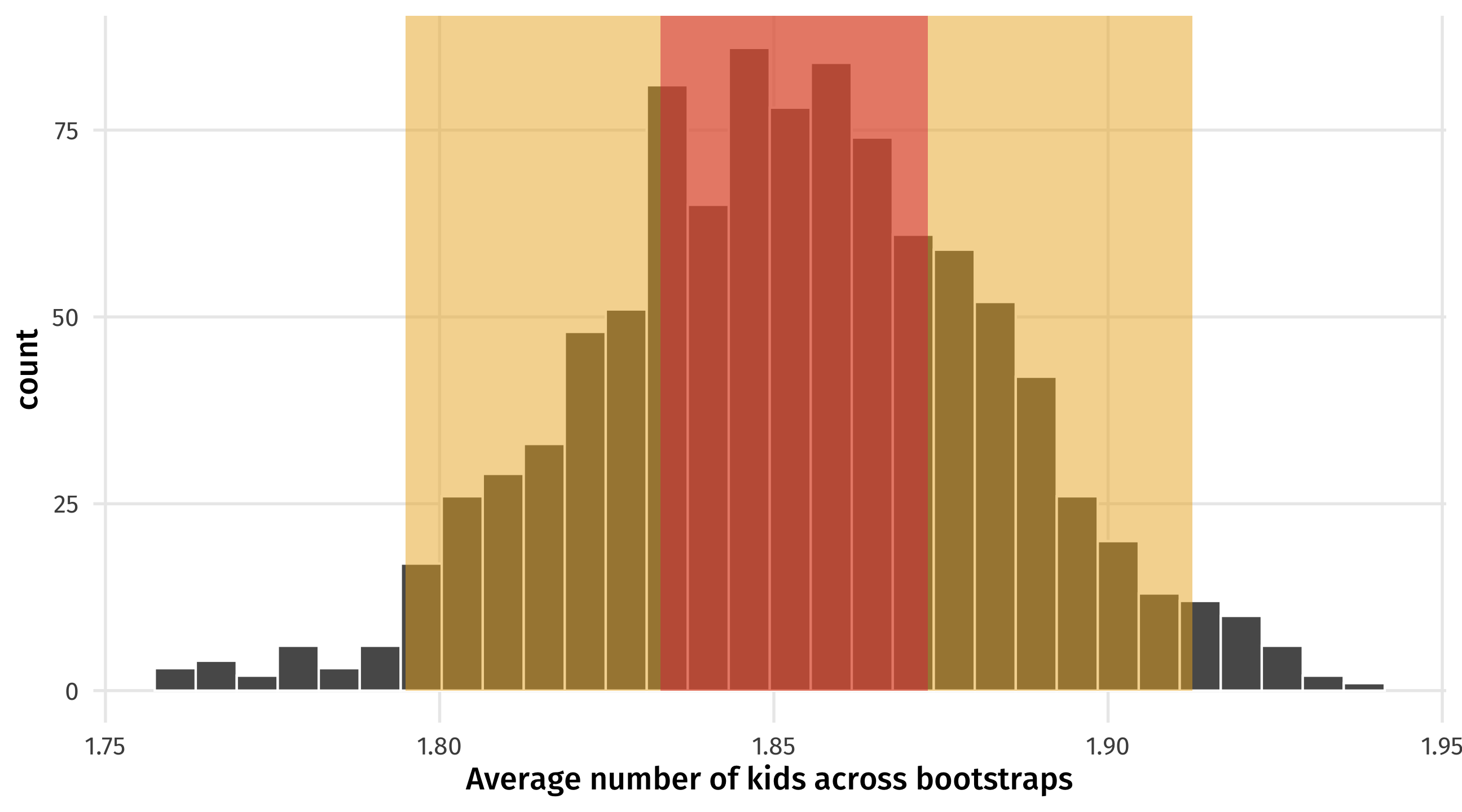
The tradeoff

You are 50% “confident” that avg. number of kids could vary between 1.83 and 1.87. Narrower range! But low confidence!
You are 95% “confident” that avg. number of kids could vary between 1.79 and 1.91. Higher range! But higher confidence!

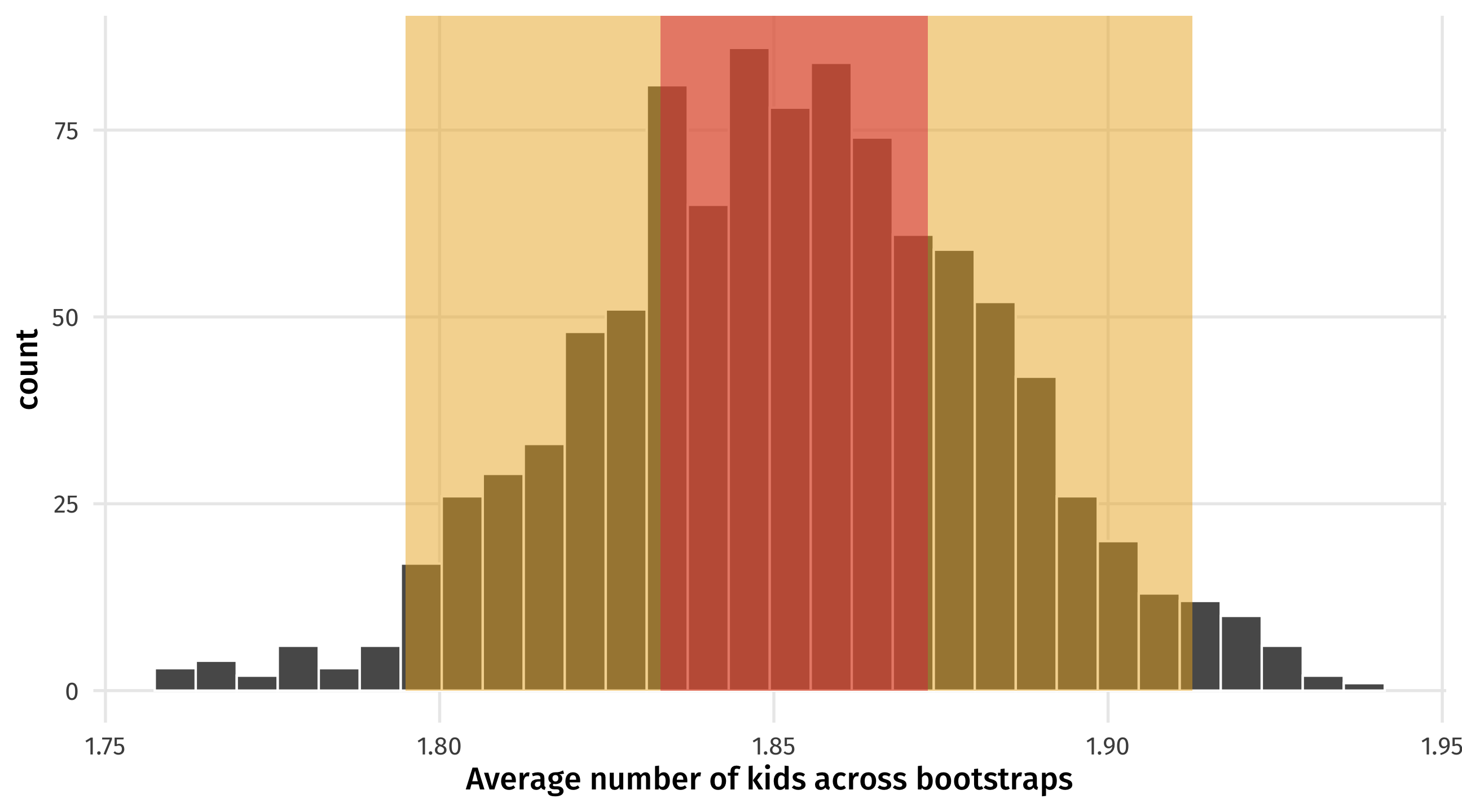
How big to make the interval?

Convention is to look at the middle 95% of the distribution

We can use the quantile() function to find the upper and lower bound of the middle 95%:

boot_kids %>% 
  summarise(low = quantile(avg_kids, .025), # middle 95% means lower bound is .025
            mean = mean(avg_kids), 
            high = quantile(avg_kids, .975)) # middle 95% means upper bound is .975

low	mean	high
1.79	1.85	1.91

The 95% confidence confidence interval for the average number of kids in the US is: (1.80, 1.91)

Mirrors of one another

The standard error and confidence interval are actually telling you the same thing

A 95% confidence interval is roughly equal to the Estimate +/- 1.96 \(\times\) standard error

boot_kids %>% 
  summarise(low = quantile(avg_kids, .025),
            mean = mean(avg_kids), 
            high = quantile(avg_kids, .975))

low	mean	high
1.79	1.85	1.91

boot_kids %>% 
  summarise(mean = mean(avg_kids), standard_error = sd(avg_kids)) %>% 
  mutate(low = mean - 1.96 * standard_error, 
         high = mean + 1.96 * standard_error) %>% 
  select(low, mean, high)

low	mean	high
1.79	1.85	1.91

🚨 Your turn: Wealth data 🚨

Look back at the wealth data

Grab your bootstrapped samples for the asset of your choosing.
Calculate the standard error and the 95% confidence interval of your best guess. Convince yourself the two can be made equivalent.

10:00