Controls

POL51

Juan Tellez

jftellez@ucdavis.edu

UC Davis

November 14, 2024

Plan for today

Controlling for confounds

Intuition

Limitations

Where are we so far?

Want to estimate the effect of X on Y

Elemental confounds get in our way

DAGs to model causal process

figure out which variables to control for and which to avoid

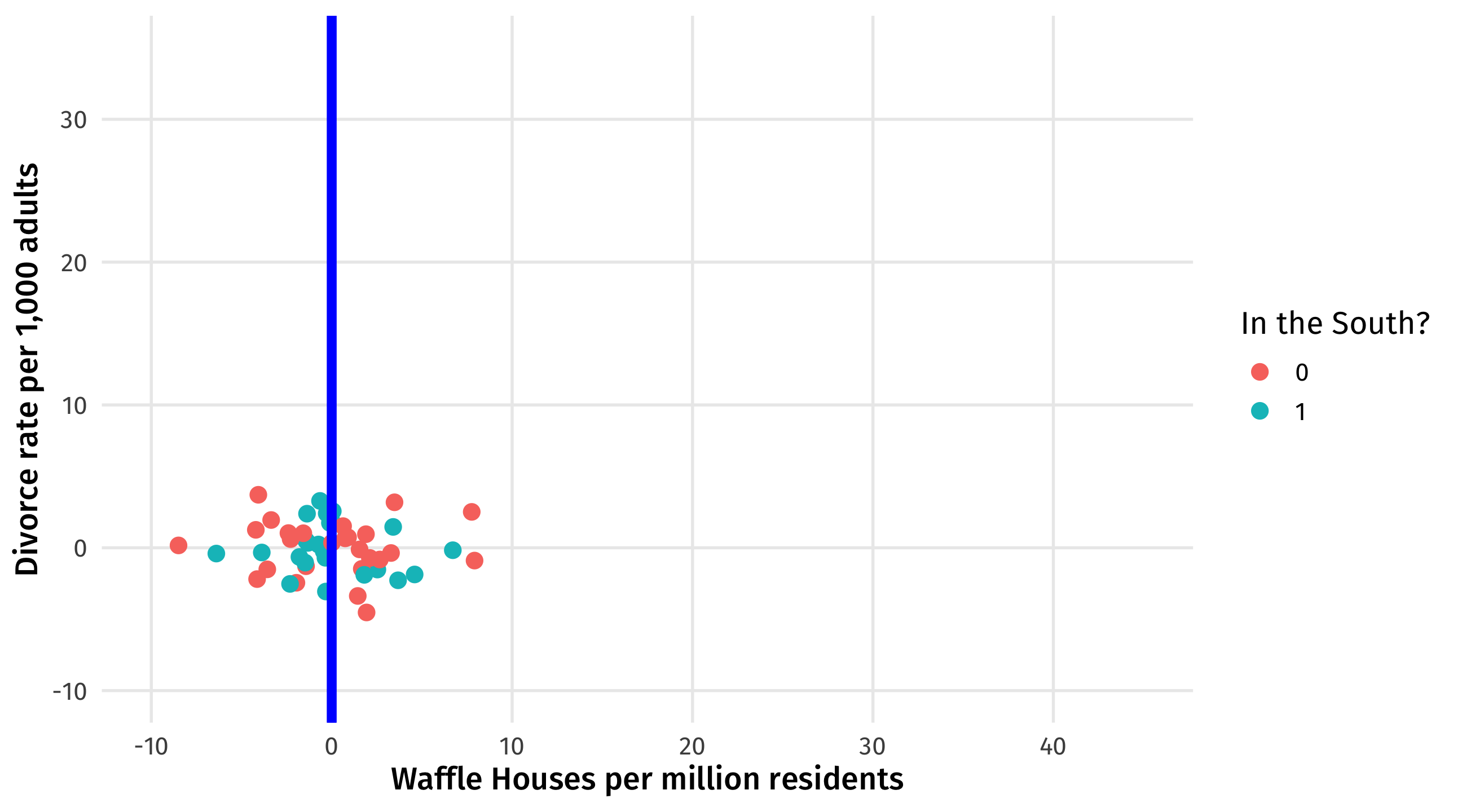
Do waffles cause divorce?

Remember, we have strong reason to believe the South is confounding the relationship between Waffle Houses and divorce rates:

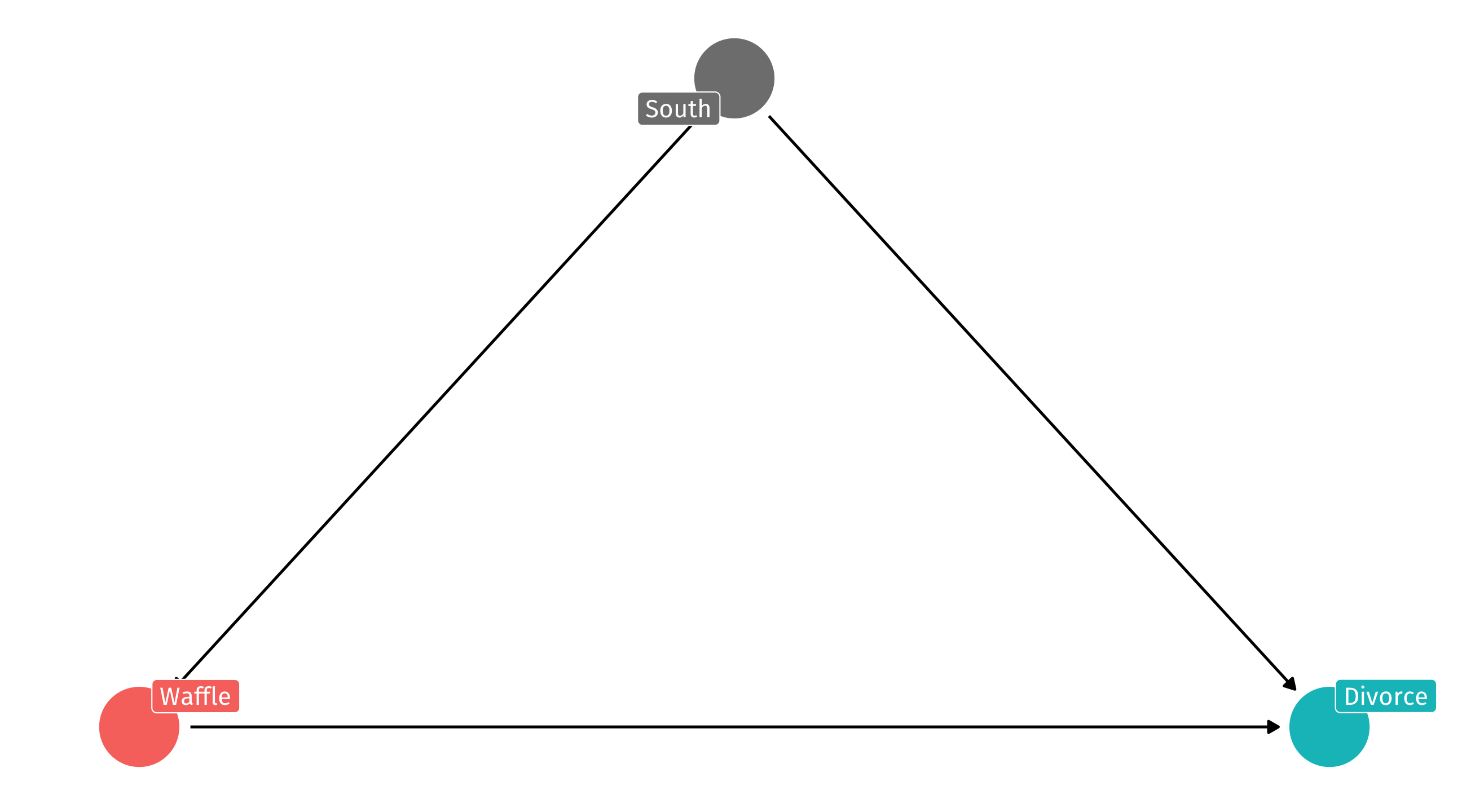
Solution

We need to control (for) the South (just like Lincoln)

It has a bad influence on divorce, waffle house locations (and the integrity of the union)

But how do we do control (for) the South? And what does that even mean?

We’ve already done it

One way to adjust/control for backdoor paths is with multiple regression:

In general: \(Y = \alpha + \beta_1X_1 + \beta_2X_2 + \dots\)

In this case: \(Y = \alpha + \beta_1Waffles + \beta_2South\)

In multiple regression, coefficients (\(\beta_i\)) are different: they describe the relationship between X1 and Y, after adjusting for the X2, X3, X4, etc.

What does it mean to control?

\(Y = \alpha + \beta_1Waffles + \beta_2South\)

Three ways of thinking about \(\color{red}{\beta_1}\) here:

The relationship between Waffles and Divorce, controlling for the South
The relationship between Waffles and Divorce that cannot be explained by the South
The relationship between Waffles and Divorce, comparing among similar states (South vs. South, North vs. North)

Does this actually work?

Only way to know for sure is with made-up data, where we know the effects ex ante:

fake = tibble(south = sample(c(0, 1), size = 50, replace = TRUE), 
              waffle = rnorm(n = 50, mean = 20, sd = 4) + 10 * south,
              divorce = rnorm(n = 50, mean = 20, sd = 2) + 8 * south)

What do we know?

fake = tibble(south = sample(c(0, 1), size = 50, replace = TRUE), 
              waffle = rnorm(n = 50, mean = 20, sd = 4) + 10*south,
              divorce = rnorm(n = 50, mean = 20, sd = 2) + 8*south)

We know that waffles have 0 effect on divorce

We know that the south has an effect of 10 on divorce

We know that the south has an effect of 8 on waffles

Controlling for the South

Fit a naive model without controls:

naive_waffles = lm(divorce ~ waffle, data = fake)
tidy(naive_waffles)

term	estimate	std.error	statistic	p.value
(Intercept)	10.3	2	5.15	4.82e-06
waffle	0.529	0.0796	6.64	2.62e-08

Our estimate is confounded: should be zero (or very close)

Controlling for the South

Fit a better model, controlling for the South:

control_waffles = lm(divorce ~ waffle + south, data = fake)
tidy(control_waffles)

term	estimate	std.error	statistic	p.value
(Intercept)	20.8	1.73	12	6.58e-16
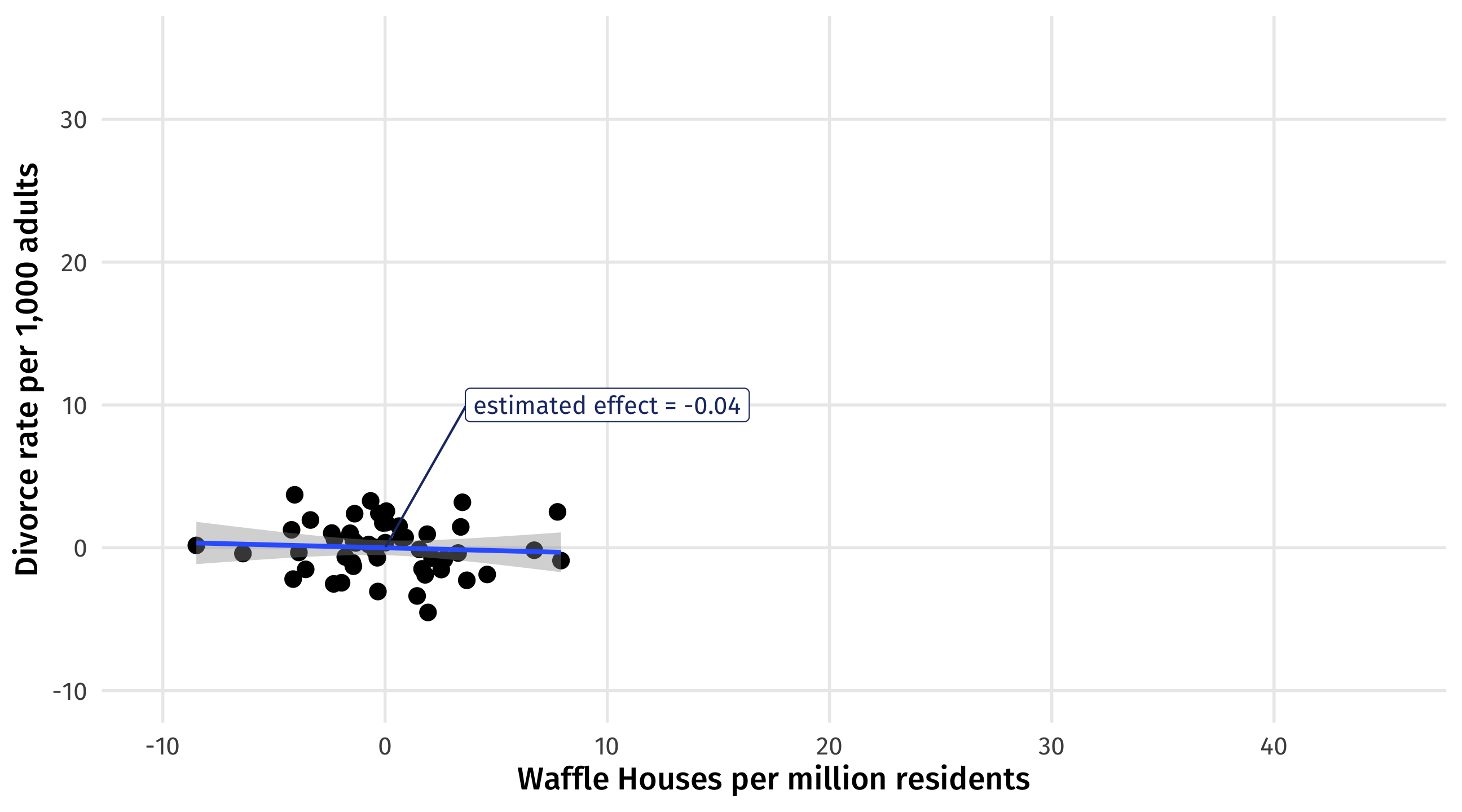
waffle	-0.0397	0.0819	-0.485	0.63
south	7.59	0.87	8.73	2.15e-11

Our estimate is closer to the truth: quite close to zero

Display the results

We can display the results in a regression table, using the huxreg() function from the huxtable package:

huxreg(naive_waffles,  control_waffles)

	(1)	(2)
(Intercept)	10.319 ***	20.808 ***
	(2.003)	(1.735)
waffle	0.529 ***	-0.040
	(0.080)	(0.082)
south		7.595 ***
		(0.870)
N	50	50
R2	0.479	0.801
logLik	-124.527	-100.445
AIC	255.054	208.891
* p < 0.001; p < 0.01; * p < 0.05.

Regression tables

Regression tables are the standard way to compare models side-by-side
Coefficient estimates, size of sample, and other info (later in course)

	(1)	(2)
(Intercept)	10.319 ***	20.808 ***
	(2.003)	(1.735)
waffle	0.529 ***	-0.040
	(0.080)	(0.082)
south		7.595 ***
		(0.870)
N	50	50
R2	0.479	0.801
logLik	-124.527	-100.445
AIC	255.054	208.891
* p < 0.001; p < 0.01; * p < 0.05.

Comparison

Model 1 has no controls: just the relationship between Waffle Houses and Divorce
Model 2 controls/adjusts for: the state being in the South
the effect of Waffle Houses on Divorce changes with controls
Model 2 estimate is smaller, closer to zero

	Naive model	Control South
(Intercept)	10.319 ***	20.808 ***
	(2.003)	(1.735)
waffle	0.529 ***	-0.040
	(0.080)	(0.082)
south		7.595 ***
		(0.870)
nobs	50	50
* p < 0.001; p < 0.01; * p < 0.05.

Interpretation

No controls: every additional Waffle House = .5 more divorces per capita
With controls: after adjusting for the South, every additional Waffle House = 0.04 fewer divorces per capita

	Naive model	Control South
(Intercept)	10.319 ***	20.808 ***
	(2.003)	(1.735)
waffle	0.529 ***	-0.040
	(0.080)	(0.082)
south		7.595 ***
		(0.870)
nobs	50	50
* p < 0.001; p < 0.01; * p < 0.05.

comparing states in the same part of the country (south / not south), every additional Waffle House = 0.04 fewer divorces per capita

Another example: 🚽 and 💰

How much does having an additional bathroom boost a house’s value?

price	bedrooms	bathrooms	sqft_living	waterfront
899000	4	2	2580	FALSE
435000	2	1	1260	FALSE
657000	4	2	2180	FALSE
590000	3	4	1970	FALSE
605000	3	2	2010	FALSE
528000	2	1	840	TRUE
315000	3	2	2500	FALSE
739900	5	2	3290	FALSE

Another example: 🚽 and 💰

A huge effect:

no_controls = lm(price ~ bathrooms, data = house_prices)
huxreg("No controls" = no_controls)

	No controls
(Intercept)	10708.309
	(6210.669)
bathrooms	250326.516 ***
	(2759.528)
N	21613
R2	0.276
logLik	-304117.741
AIC	608241.481
* p < 0.001; p < 0.01; * p < 0.05.

The problem

We are comparing houses with more and fewer bathrooms. But houses with more bathrooms tend to be larger! So house size is confounding the relationship between 🚽 and 💰

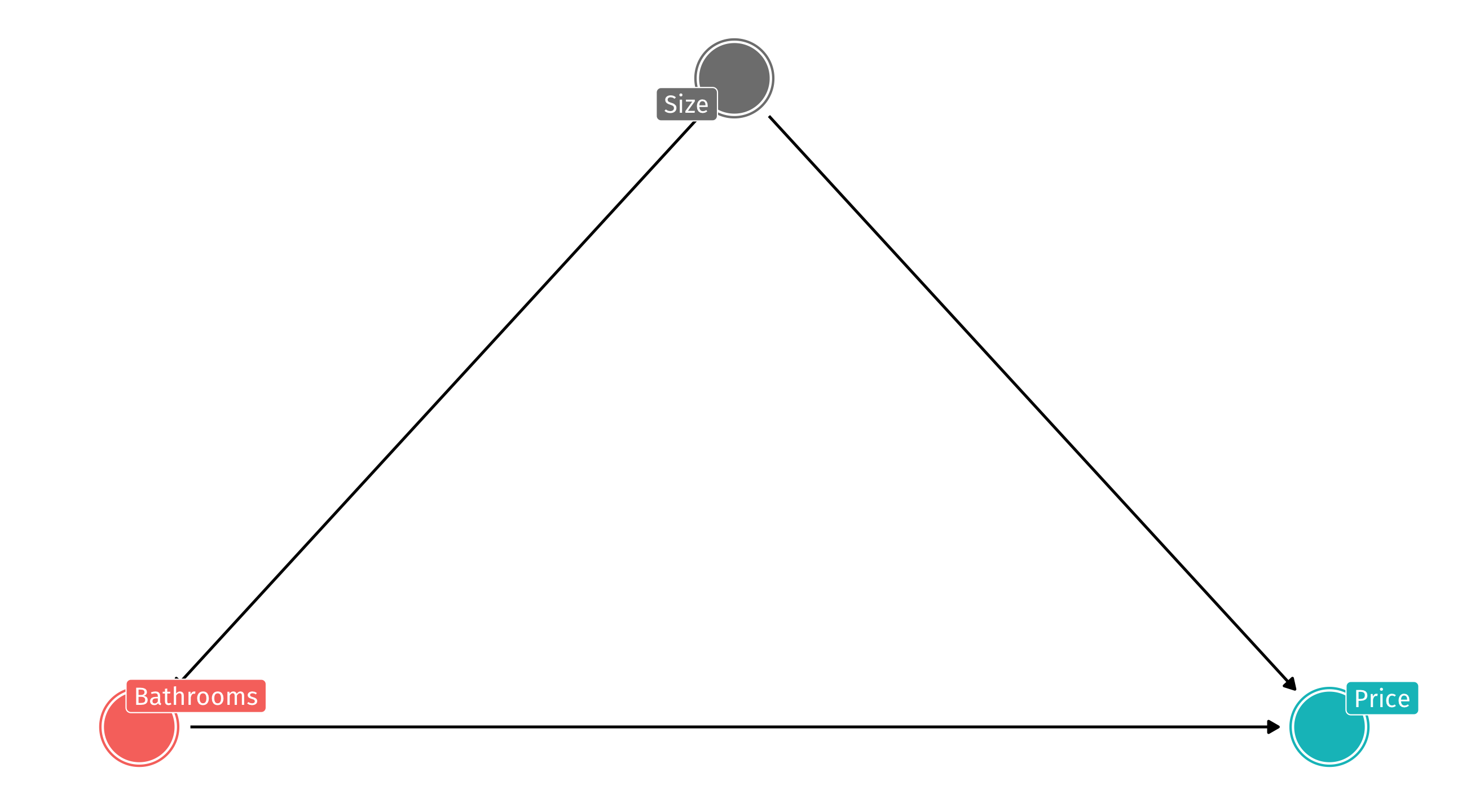
What happens if we control for how large a house is?

controls = lm(price ~ bathrooms + sqft_living, data = house_prices)
huxreg("No controls" = no_controls, "Controls" = controls)

	No controls	Controls
(Intercept)	10708.309	-39456.614 ***
	(6210.669)	(5223.129)
bathrooms	250326.516 ***	-5164.600
	(2759.528)	(3519.452)
sqft_living		283.892 ***
		(2.951)
N	21613	21613
R2	0.276	0.493
logLik	-304117.741	-300266.206
AIC	608241.481	600540.413
* p < 0.001; p < 0.01; * p < 0.05.

What happens if we control for how large a house is?

	No controls	Controls
(Intercept)	10708.309	-39456.614 ***
	(6210.669)	(5223.129)
bathrooms	250326.516 ***	-5164.600
	(2759.528)	(3519.452)
sqft_living		283.892 ***
		(2.951)
nobs	21613	21613
* p < 0.001; p < 0.01; * p < 0.05.

adjusting for size, additional bathrooms have a much smaller (even negative!) relationship to price

What’s going on?

In our made-up world, if we control for the South we can get back the uncounfounded estimate of Divorce ~ Waffles

But what’s lm() doing under-the-hood that makes this possible?

What’s going on?

lm() is estimating \(South \rightarrow Divorce\) and \(South \rightarrow Waffles\)
it is then subtracting out or removing the effect of South on Divorce and Waffles
what’s left is the relationship between Waffles and Divorce, adjusting for the influence of the South on each

Visualizing controlling for the South

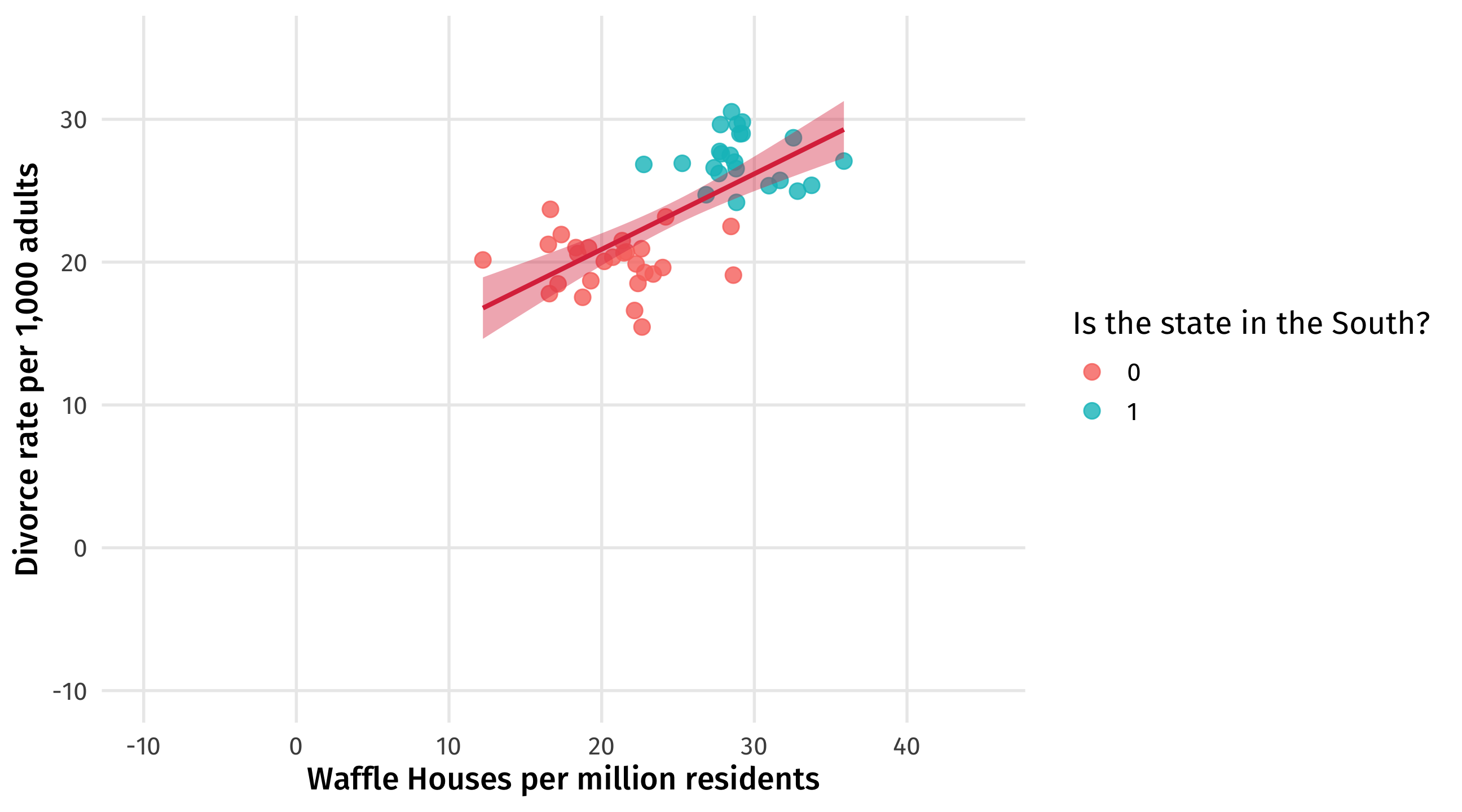
This is the confounded relationship between waffles and divorce (zoomed out)

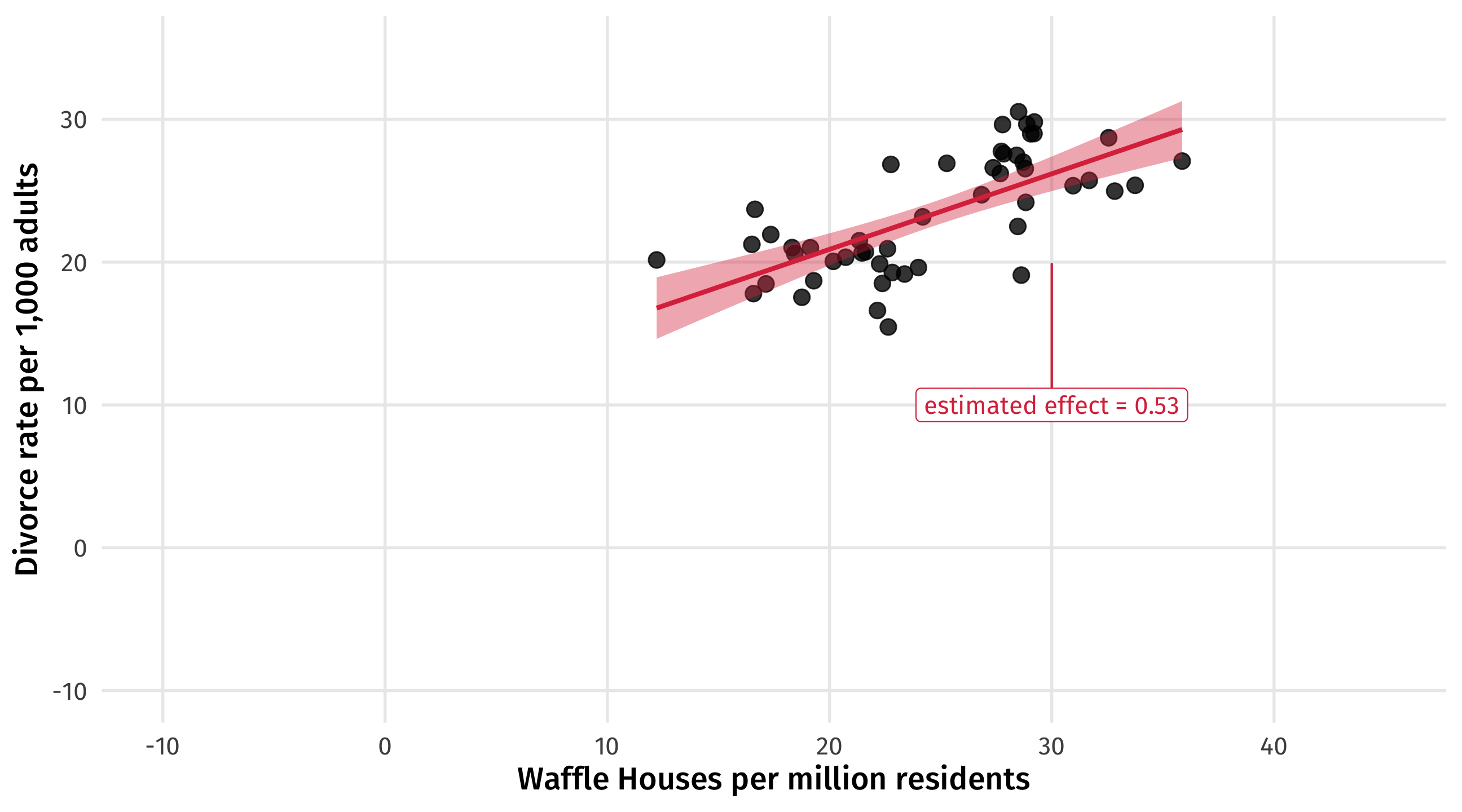
Add the south

We can see what we already know: states in the South tend to have more divorce, and more waffles

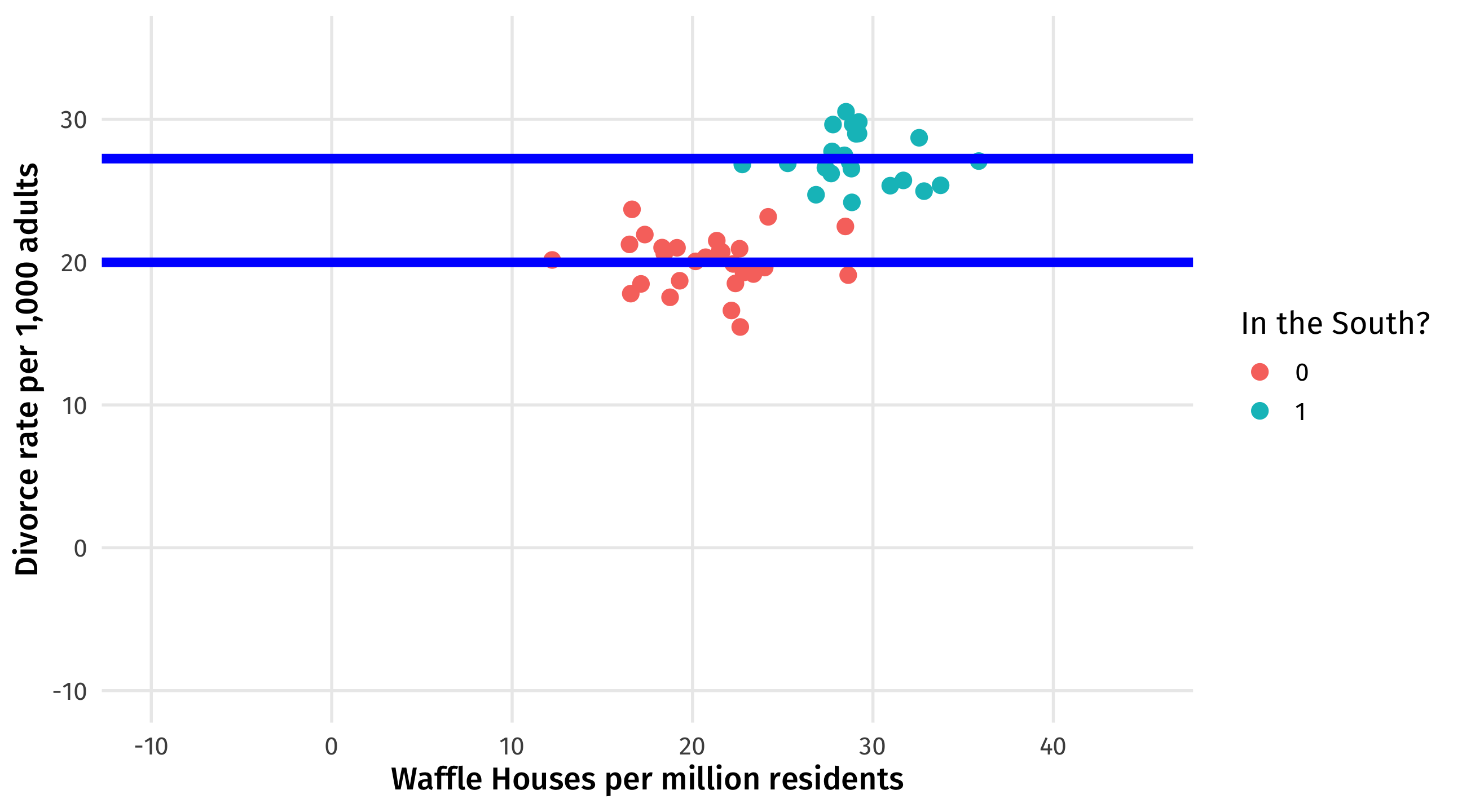
Effect of south on divorce

\(South \rightarrow Divorce = 10\) How much higher, on average, divorce is in the South than the North

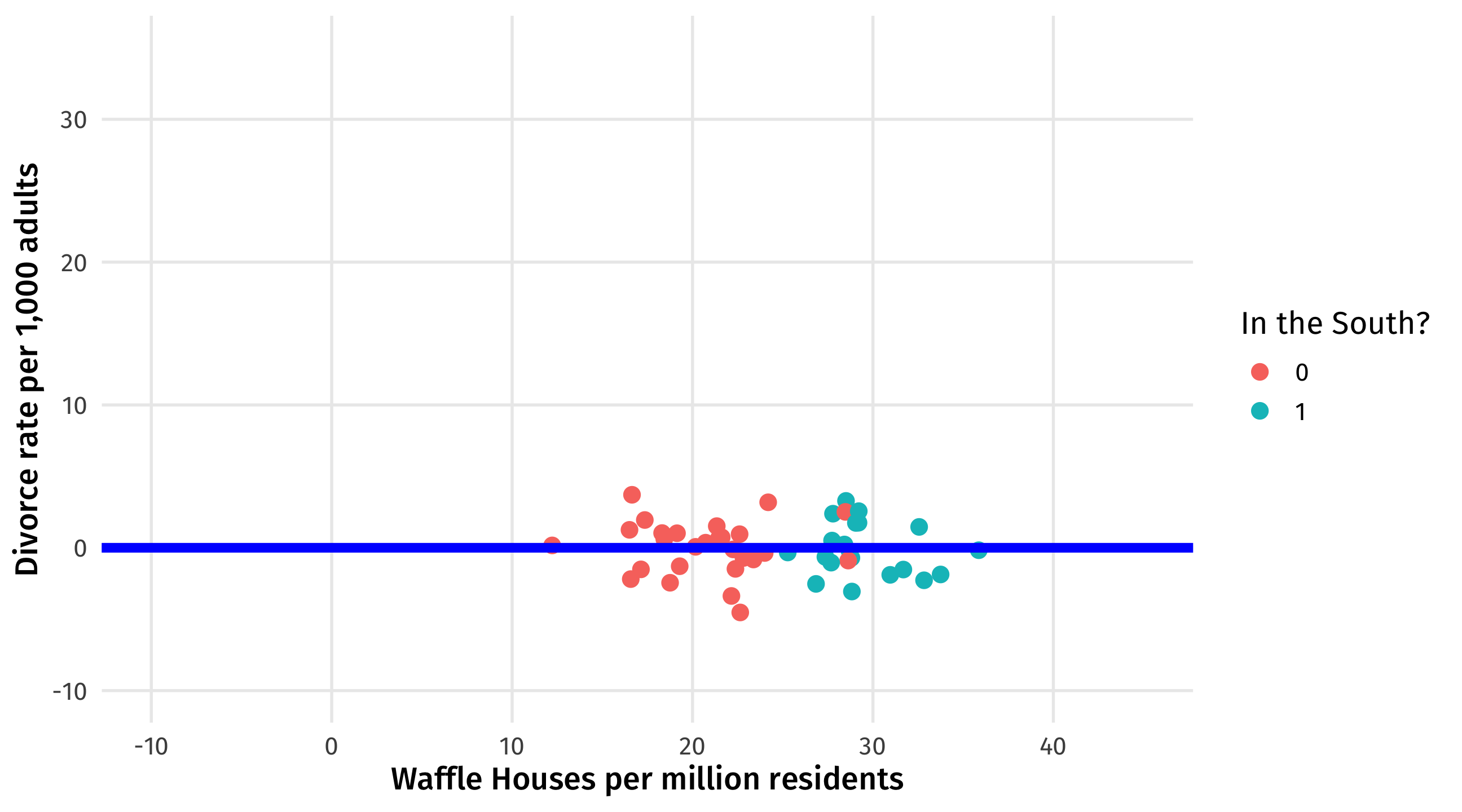
Remove effect of South on divorce

Regression subtracts out the effect of the South on divorce

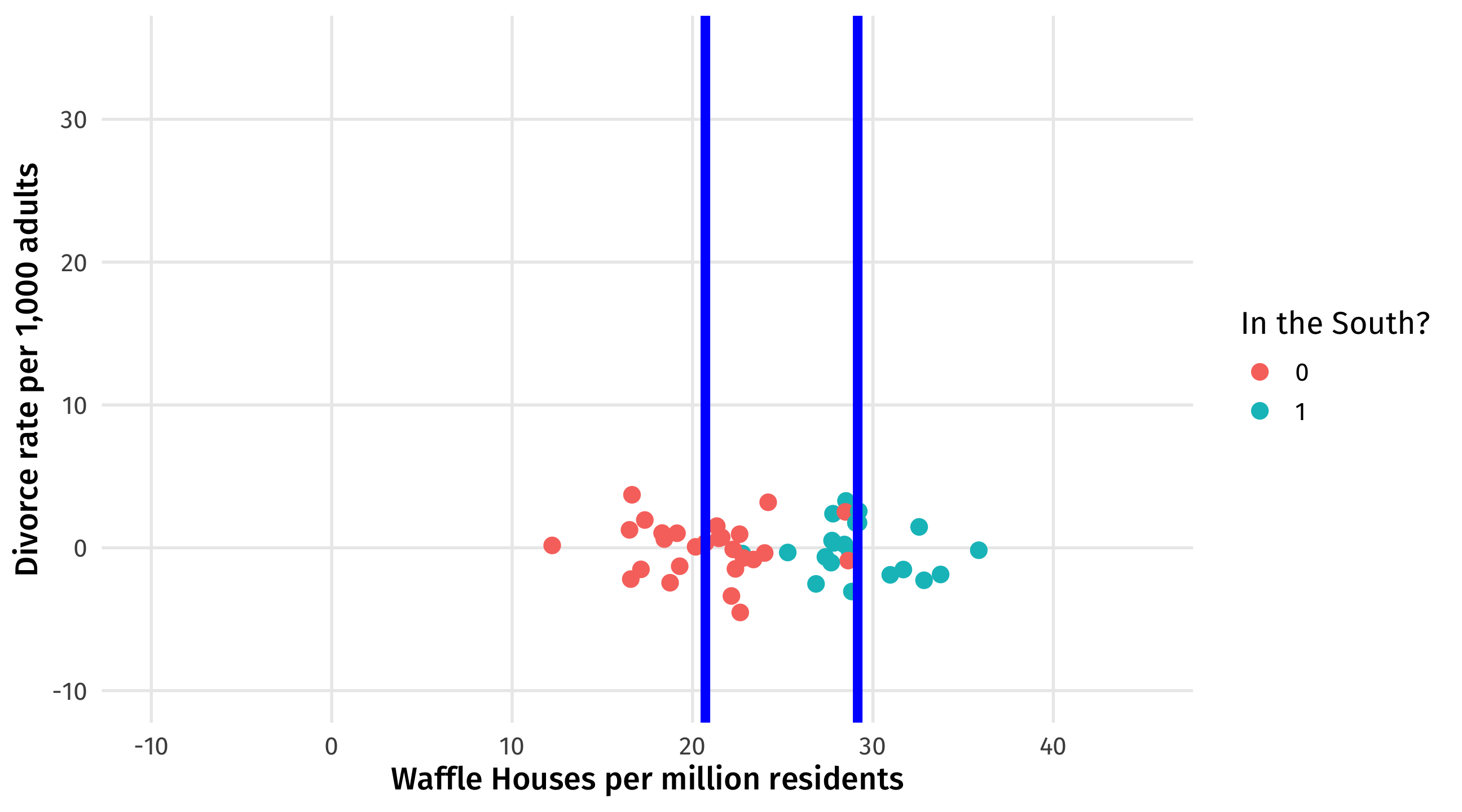
Next: effect of South on waffles

\(South \rightarrow Waffles = 8\) How many more, on average, Waffle Houses there are in the South than the North

Subtract out the effect of south on waffles

Regression subtracts out the effect of the South on waffles

What’s left over?

The true effect of waffles on divorce \(\approx\) 0

The other confounds

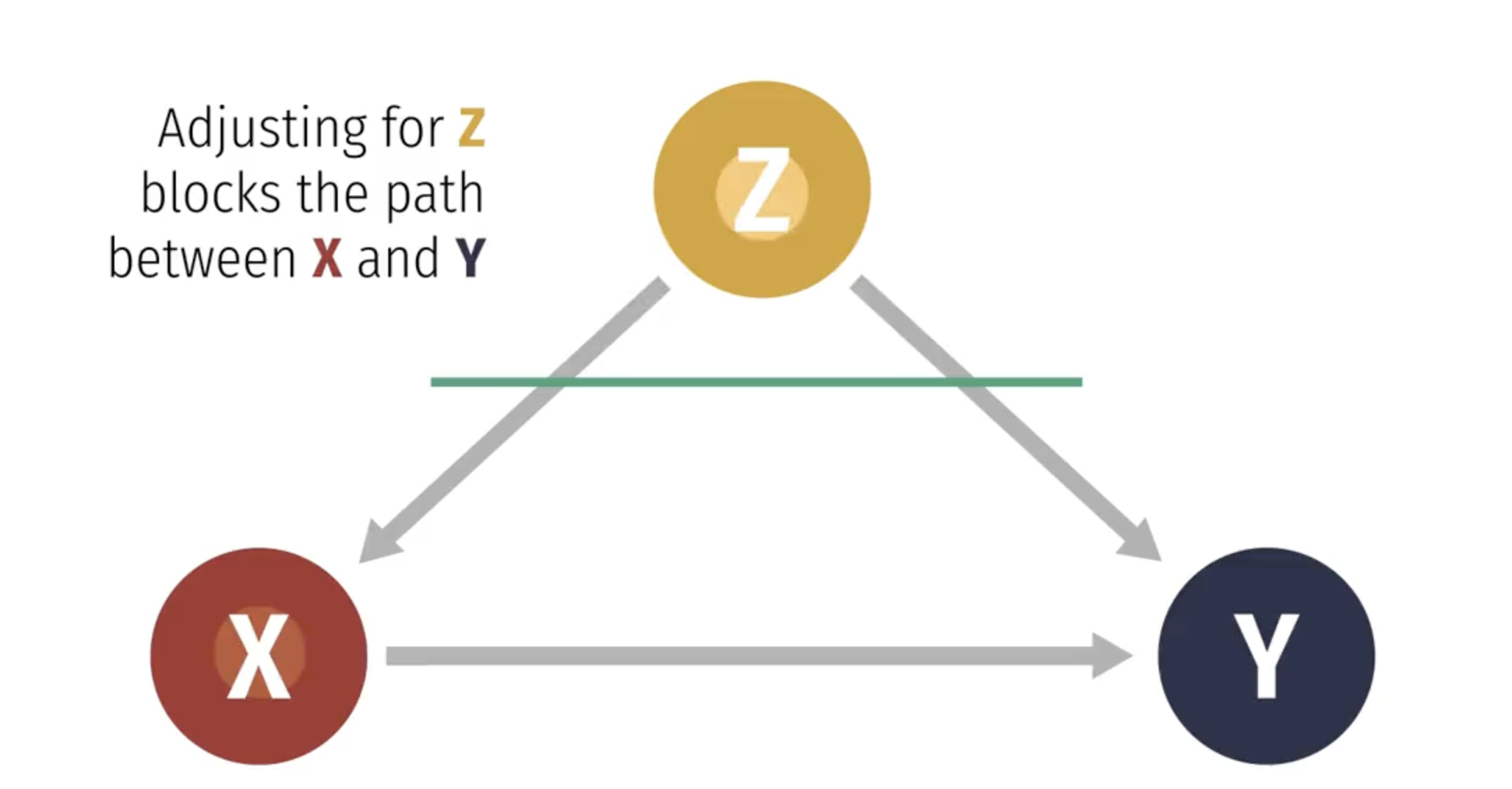
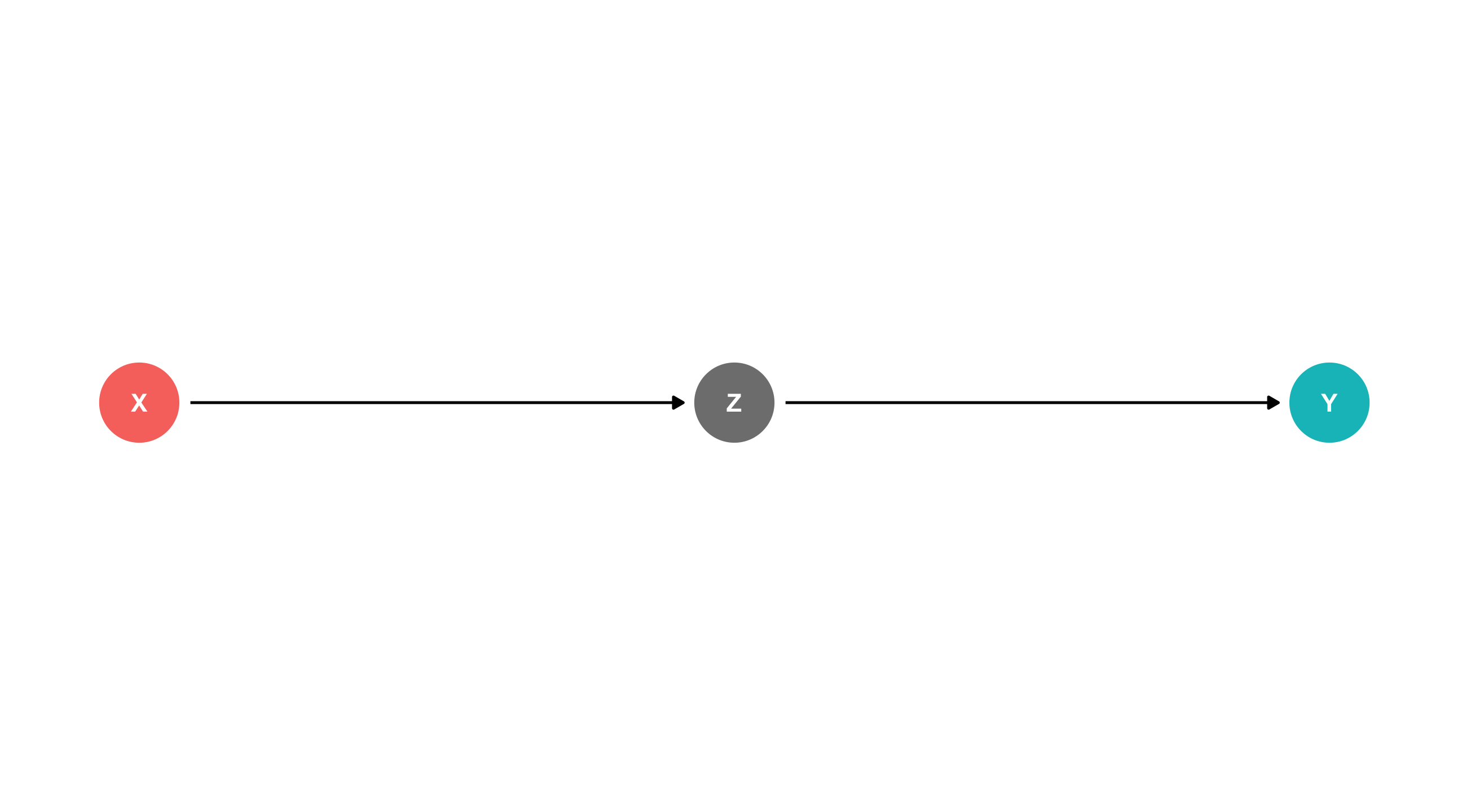
The perplexing pipe

Remember, with a perplexing pipe, controlling for Z blocks the effect of X on Y:

Simulation

Let’s make up some data to show this: every unit of foreign aid increases corruption by 8; every unit of corruption increases the number of protest by 4

fake_pipe = tibble(aid = rnorm(n = 200, mean = 10), 
                   corruption = rnorm(n = 200, mean = 10) + 8 * aid, 
                   protest = rnorm(n = 200, mean = 10) + 4 * corruption)

What is the true effect of aid on protest? Tricky since the effect runs through corruption

For every unit of aid, corruption increases by 8; and for every unit of corruption, protest increases by 4…

The effect of aid on protest is \(4 \times 8 = 32\)

The data

aid	corruption	protest
10.89	96.18	394.09
10.71	96.07	396.25
9.43	82.24	339.30
13.60	119.00	486.65
9.35	83.47	340.71
9.34	83.46	343.73

Bad controls

Remember, with a pipe controlling for Z (corruption) is a bad idea

Let’s fit two models, where one makes the mistake of controlling for corruption

right_model = lm(protest ~ aid, data = fake_pipe)
bad_control = lm(protest ~ aid + corruption, data = fake_pipe)

Bad controls

Notice how the model that mistakenly controls for Z tells you that X basically has no effect on Y (wrong)
The model that doesn’t control for Z is closer to the truth

	Correct model	Bad control
(Intercept)	43.805 ***	8.595 ***
	(2.957)	(0.966)
aid	32.583 ***	-0.530
	(0.293)	(0.602)
corruption		4.075 ***
		(0.074)
nobs	200	200
* p < 0.001; p < 0.01; * p < 0.05.

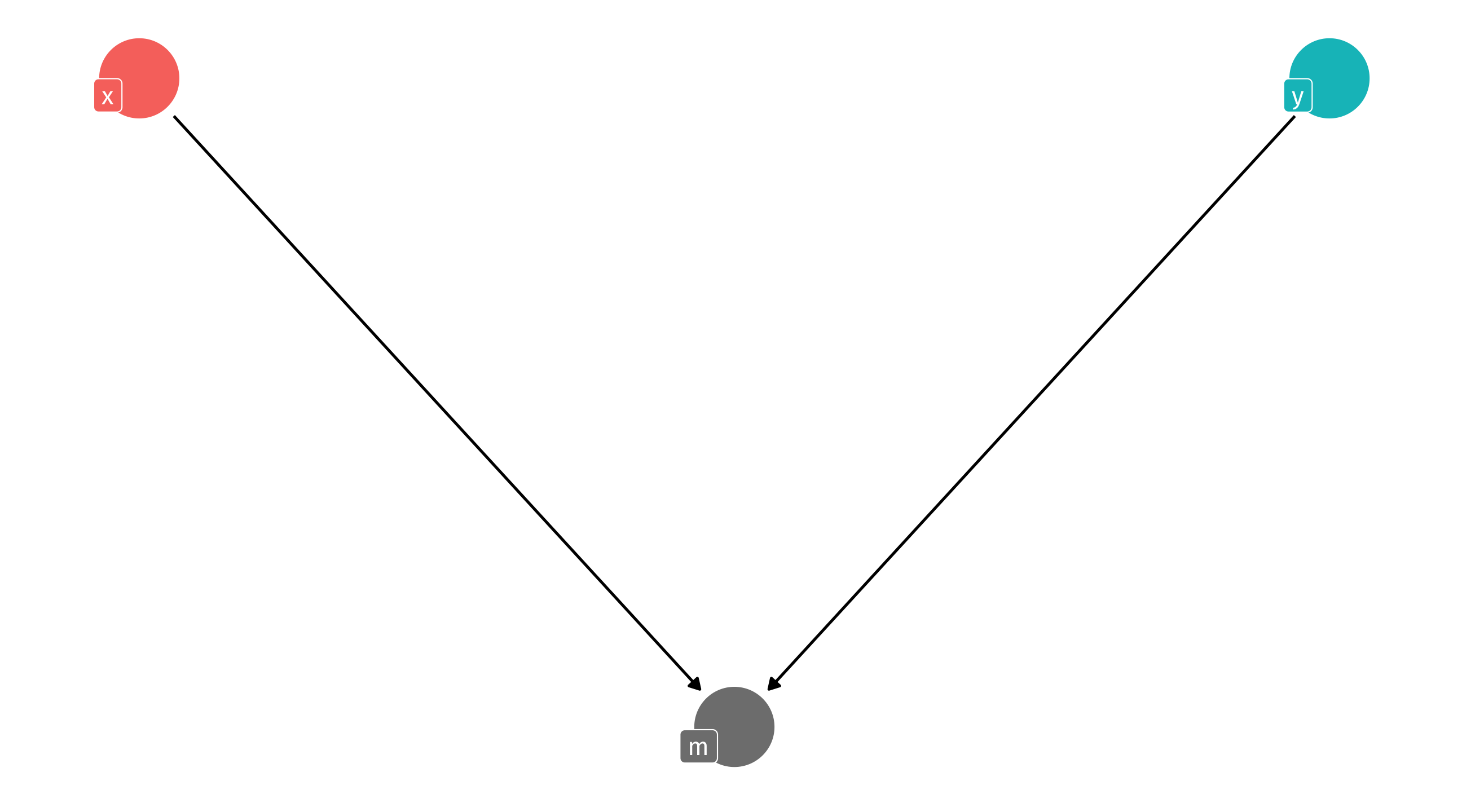
The exploding collider

Remember, with an exploding collider, controlling for M creates strange correlations between X and Y:

Simulation

Let’s make up some data to show this:

fake_collider = tibble(x = rnorm(n = 100, mean = 10), 
                   y = rnorm(n = 100, mean = 10),
                   m = rnorm(n = 100, mean = 10) + 8 * x + 4 * y)

X has an effect of 8 on M
Y has an effect of 4 on M
X has no effect on Y

The data

x	y	m
9.765385	9.714265	127.0328
12.082301	10.857936	149.0461
7.940696	8.910833	107.3517
9.894526	10.810412	132.0944
9.943018	10.676781	132.3096
11.200857	10.711525	141.5535

Bad controls

What’s the true effect of X on Y? it’s zero

Remember, with a collider controlling for M is a bad idea

Let’s fit two models, where one makes the mistake of controlling for M

right_model = lm(y ~ x, data = fake_collider)
collided_model = lm(y ~ x + m, data = fake_collider)

Bad controls

Notice how the model that mistakenly controls for M tells you that X has a strong, negative effect on Y (wrong)
The model that doesn’t control for M is closer to the truth

	Correct model	Collided!
(Intercept)	9.235 ***	-2.513 ***
	(0.824)	(0.345)
x	0.088	-1.969 ***
	(0.083)	(0.054)
m		0.248 ***
		(0.006)
nobs	100	100
* p < 0.001; p < 0.01; * p < 0.05.

Colliding as sample selection

Most of the time when we see a collider, it’s because we’re looking at a weird sample of the population we’re interested in

Examples: the non-relationship between height and scoring, among NBA players; the (alleged) negative correlation between how surprising and reliable findings are, among published research

Hiring at Google

Imagine Google wants to hire the best of the best, and they have two criteria: interpersonal skills, and technical skills

Say Google can measure how socially and technically skilled someone is (0-100)

fake_google = tibble(social_skills = rnorm(n = 200, mean = 50, sd = 10), 
                     tech_skills = rnorm(n = 200, mean = 50, sd = 10))

The two are causally unrelated: one does not affect the other; improving someone’s social skills would not hurt their technical skills

The data

social_skills	tech_skills
68.75	62.41
46.25	36.08
42.20	64.85
50.82	39.91
48.28	66.39
38.20	53.77
54.25	49.62
40.50	36.41

Simulate the hiring process

Now imagine that they add up the two skills to see a person’s overall quality:

fake_google %>% 
  mutate(total_score = social_skills + tech_skills)

social_skills	tech_skills	total_score
42	53.9	95.9
52.2	45.9	98.1
44.1	22.1	66.2
45.8	58.9	105
49.6	57.6	107
46.3	52.7	99
50.9	50.9	102
32.8	56.5	89.3
33.9	41	74.9
59	37.6	96.6
59.4	43.7	103
60.8	53.3	114
48.9	76.6	125
43.7	41.9	85.6
55.3	43.3	98.7
50.2	41	91.2
50.6	53	104
61.4	50	111
53	53	106
38.6	47.8	86.3
36.2	53.8	90
50.4	64.6	115
42.4	59.5	102
50.2	47.8	98
42.6	64.9	107
44.5	44.7	89.2
40.7	60.7	101
45.6	52.2	97.8
51.5	46.4	97.9
65.3	35.5	101
45.1	32.2	77.3
65	57.5	122
58.7	71.9	131
54.2	49.6	104
40.5	49.4	89.9
44.7	51.8	96.5
58.3	50.9	109
48.3	66.4	115
51.4	52.7	104
41.8	42.7	84.5
41.5	49.1	90.6
60	47.2	107
40.4	54.9	95.3
65.4	50.5	116
53.5	54.5	108
50.8	46.3	97.2
43.5	54.3	97.8
58.1	38.8	96.9
57.5	55	113
47.6	34.9	82.5
58	49.1	107
61	47.6	109
52.3	40.2	92.5
49.7	64.4	114
33.5	42.6	76.1
39.4	59	98.4
59	52.1	111
41.1	36.5	77.6
39.8	62.1	102
38.8	57.8	96.6
36.1	62.6	98.7
42.2	64.8	107
29.5	34.4	63.9
43.6	51.9	95.5
46.1	48.4	94.5
52.6	58.1	111
60.5	49.9	110
46.4	54.2	101
45.1	40.1	85.2
47	59	106
42	35.4	77.5
68.7	62.4	131
39.2	52.1	91.3
65.4	33	98.4
48.6	45.1	93.7
45.8	56.5	102
27.9	52.5	80.4
48.2	56.9	105
52.9	44.4	97.3
42.4	59.9	102
52.5	42.7	95.1
32.9	44.5	77.4
44.7	39.2	83.9
52.1	48	100
42.4	46.4	88.8
54.1	57.7	112
45.9	49.2	95.1
57.8	51.9	110
40.5	36.4	76.9
37	60.5	97.5
39.5	48.6	88.1
53.2	53.5	107
53.2	47.8	101
49.4	40.4	89.7
68.9	51.1	120
56.6	35.3	91.9
41.3	51.3	92.6
56.5	52.6	109
52.3	51.5	104
62.1	34.9	97
30	61.2	91.2
53.7	29.9	83.5
57.7	53.8	112
56.4	44.9	101
50.8	39.9	90.7
40	59.5	99.5
59.3	34.8	94.1
46.6	58.4	105
43.2	32.5	75.7
40.9	51.9	92.7
49.2	66	115
58.4	54.9	113
46.9	51.6	98.6
58.2	47.2	105
48.8	33.6	82.3
47.1	68	115
38.6	61.2	99.8
53.9	52.1	106
42	40.5	82.5
43.6	46.4	90
44.5	41.3	85.8
46.2	36.1	82.3
56.8	41.1	97.9
48.9	57.1	106
56.7	60.6	117
54.5	33.7	88.2
46.9	54.3	101
63.9	58.4	122
50.2	52.9	103
55.5	57.8	113
58.7	55.7	114
37.5	58.1	95.6
60	49.9	110
76.2	36.5	113
39.2	52.7	91.9
50.1	59.4	110
63.6	63.3	127
59.5	44.6	104
24.1	58.1	82.2
57.4	51.3	109
68.2	47.3	116
46.2	43.3	89.5
59.6	40.8	100
39.3	53.6	92.9
62	50.3	112
45.7	50.4	96
42.2	55.1	97.3
54.1	40.7	94.8
48.1	64.5	113
49.4	47.7	97.1
37.7	63.2	101
47.2	52.2	99.4
54.4	41.7	96.1
59.3	46.2	106
50.9	31	81.9
46.4	73.9	120
34.6	49.4	84
51.3	45	96.3
40	52.1	92.1
51.6	32.4	84
35.3	49	84.2
36.6	30.8	67.4
64.2	56.4	121
44.5	56.4	101
38.4	32.1	70.5
58.3	48.7	107
64.6	44.5	109
49.6	55.2	105
57.1	45.5	103
35.3	51.8	87.1
44.7	40.4	85.1
58.5	58.3	117
43.5	42.4	85.9
45.7	56.3	102
49.5	57.7	107
47.8	51.4	99.2
51	67	118
38.3	35	73.3
54.1	41.9	96
47.9	55.7	104
44.4	36.2	80.6
63.2	50.3	114
50.8	39.9	90.7
38.2	53.8	92
58.1	42.2	100
59.8	55.2	115
41	31.9	72.8
54.3	40.6	94.9
49.6	54.4	104
47.2	51	98.1
57.5	67.9	125
39.3	57.4	96.7
51.5	56	108
48.5	39.4	87.9
45.3	61	106
51.7	41.7	93.4
49.7	46.4	96.1
44.9	52.5	97.4
37.2	43.6	80.8
50.7	39.1	89.8

Simulating the hiring process

Now imagine that Google only hires people who are in the top 15% of quality (in this case that’s 112.8 or higher)

social_skills	tech_skills	total_score	hired
42	53.9	95.9	no
52.2	45.9	98.1	no
44.1	22.1	66.2	no
45.8	58.9	105	no
49.6	57.6	107	no
46.3	52.7	99	no
50.9	50.9	102	no
32.8	56.5	89.3	no
33.9	41	74.9	no
59	37.6	96.6	no
59.4	43.7	103	no
60.8	53.3	114	yes
48.9	76.6	125	yes
43.7	41.9	85.6	no
55.3	43.3	98.7	no
50.2	41	91.2	no
50.6	53	104	no
61.4	50	111	no
53	53	106	no
38.6	47.8	86.3	no
36.2	53.8	90	no
50.4	64.6	115	yes
42.4	59.5	102	no
50.2	47.8	98	no
42.6	64.9	107	no
44.5	44.7	89.2	no
40.7	60.7	101	no
45.6	52.2	97.8	no
51.5	46.4	97.9	no
65.3	35.5	101	no
45.1	32.2	77.3	no
65	57.5	122	yes
58.7	71.9	131	yes
54.2	49.6	104	no
40.5	49.4	89.9	no
44.7	51.8	96.5	no
58.3	50.9	109	no
48.3	66.4	115	yes
51.4	52.7	104	no
41.8	42.7	84.5	no
41.5	49.1	90.6	no
60	47.2	107	no
40.4	54.9	95.3	no
65.4	50.5	116	yes
53.5	54.5	108	no
50.8	46.3	97.2	no
43.5	54.3	97.8	no
58.1	38.8	96.9	no
57.5	55	113	yes
47.6	34.9	82.5	no
58	49.1	107	no
61	47.6	109	no
52.3	40.2	92.5	no
49.7	64.4	114	yes
33.5	42.6	76.1	no
39.4	59	98.4	no
59	52.1	111	no
41.1	36.5	77.6	no
39.8	62.1	102	no
38.8	57.8	96.6	no
36.1	62.6	98.7	no
42.2	64.8	107	no
29.5	34.4	63.9	no
43.6	51.9	95.5	no
46.1	48.4	94.5	no
52.6	58.1	111	no
60.5	49.9	110	no
46.4	54.2	101	no
45.1	40.1	85.2	no
47	59	106	no
42	35.4	77.5	no
68.7	62.4	131	yes
39.2	52.1	91.3	no
65.4	33	98.4	no
48.6	45.1	93.7	no
45.8	56.5	102	no
27.9	52.5	80.4	no
48.2	56.9	105	no
52.9	44.4	97.3	no
42.4	59.9	102	no
52.5	42.7	95.1	no
32.9	44.5	77.4	no
44.7	39.2	83.9	no
52.1	48	100	no
42.4	46.4	88.8	no
54.1	57.7	112	no
45.9	49.2	95.1	no
57.8	51.9	110	no
40.5	36.4	76.9	no
37	60.5	97.5	no
39.5	48.6	88.1	no
53.2	53.5	107	no
53.2	47.8	101	no
49.4	40.4	89.7	no
68.9	51.1	120	yes
56.6	35.3	91.9	no
41.3	51.3	92.6	no
56.5	52.6	109	no
52.3	51.5	104	no
62.1	34.9	97	no
30	61.2	91.2	no
53.7	29.9	83.5	no
57.7	53.8	112	no
56.4	44.9	101	no
50.8	39.9	90.7	no
40	59.5	99.5	no
59.3	34.8	94.1	no
46.6	58.4	105	no
43.2	32.5	75.7	no
40.9	51.9	92.7	no
49.2	66	115	yes
58.4	54.9	113	yes
46.9	51.6	98.6	no
58.2	47.2	105	no
48.8	33.6	82.3	no
47.1	68	115	yes
38.6	61.2	99.8	no
53.9	52.1	106	no
42	40.5	82.5	no
43.6	46.4	90	no
44.5	41.3	85.8	no
46.2	36.1	82.3	no
56.8	41.1	97.9	no
48.9	57.1	106	no
56.7	60.6	117	yes
54.5	33.7	88.2	no
46.9	54.3	101	no
63.9	58.4	122	yes
50.2	52.9	103	no
55.5	57.8	113	yes
58.7	55.7	114	yes
37.5	58.1	95.6	no
60	49.9	110	no
76.2	36.5	113	yes
39.2	52.7	91.9	no
50.1	59.4	110	no
63.6	63.3	127	yes
59.5	44.6	104	no
24.1	58.1	82.2	no
57.4	51.3	109	no
68.2	47.3	116	yes
46.2	43.3	89.5	no
59.6	40.8	100	no
39.3	53.6	92.9	no
62	50.3	112	yes
45.7	50.4	96	no
42.2	55.1	97.3	no
54.1	40.7	94.8	no
48.1	64.5	113	yes
49.4	47.7	97.1	no
37.7	63.2	101	no
47.2	52.2	99.4	no
54.4	41.7	96.1	no
59.3	46.2	106	no
50.9	31	81.9	no
46.4	73.9	120	yes
34.6	49.4	84	no
51.3	45	96.3	no
40	52.1	92.1	no
51.6	32.4	84	no
35.3	49	84.2	no
36.6	30.8	67.4	no
64.2	56.4	121	yes
44.5	56.4	101	no
38.4	32.1	70.5	no
58.3	48.7	107	no
64.6	44.5	109	no
49.6	55.2	105	no
57.1	45.5	103	no
35.3	51.8	87.1	no
44.7	40.4	85.1	no
58.5	58.3	117	yes
43.5	42.4	85.9	no
45.7	56.3	102	no
49.5	57.7	107	no
47.8	51.4	99.2	no
51	67	118	yes
38.3	35	73.3	no
54.1	41.9	96	no
47.9	55.7	104	no
44.4	36.2	80.6	no
63.2	50.3	114	yes
50.8	39.9	90.7	no
38.2	53.8	92	no
58.1	42.2	100	no
59.8	55.2	115	yes
41	31.9	72.8	no
54.3	40.6	94.9	no
49.6	54.4	104	no
47.2	51	98.1	no
57.5	67.9	125	yes
39.3	57.4	96.7	no
51.5	56	108	no
48.5	39.4	87.9	no
45.3	61	106	no
51.7	41.7	93.4	no
49.7	46.4	96.1	no
44.9	52.5	97.4	no
37.2	43.6	80.8	no
50.7	39.1	89.8	no

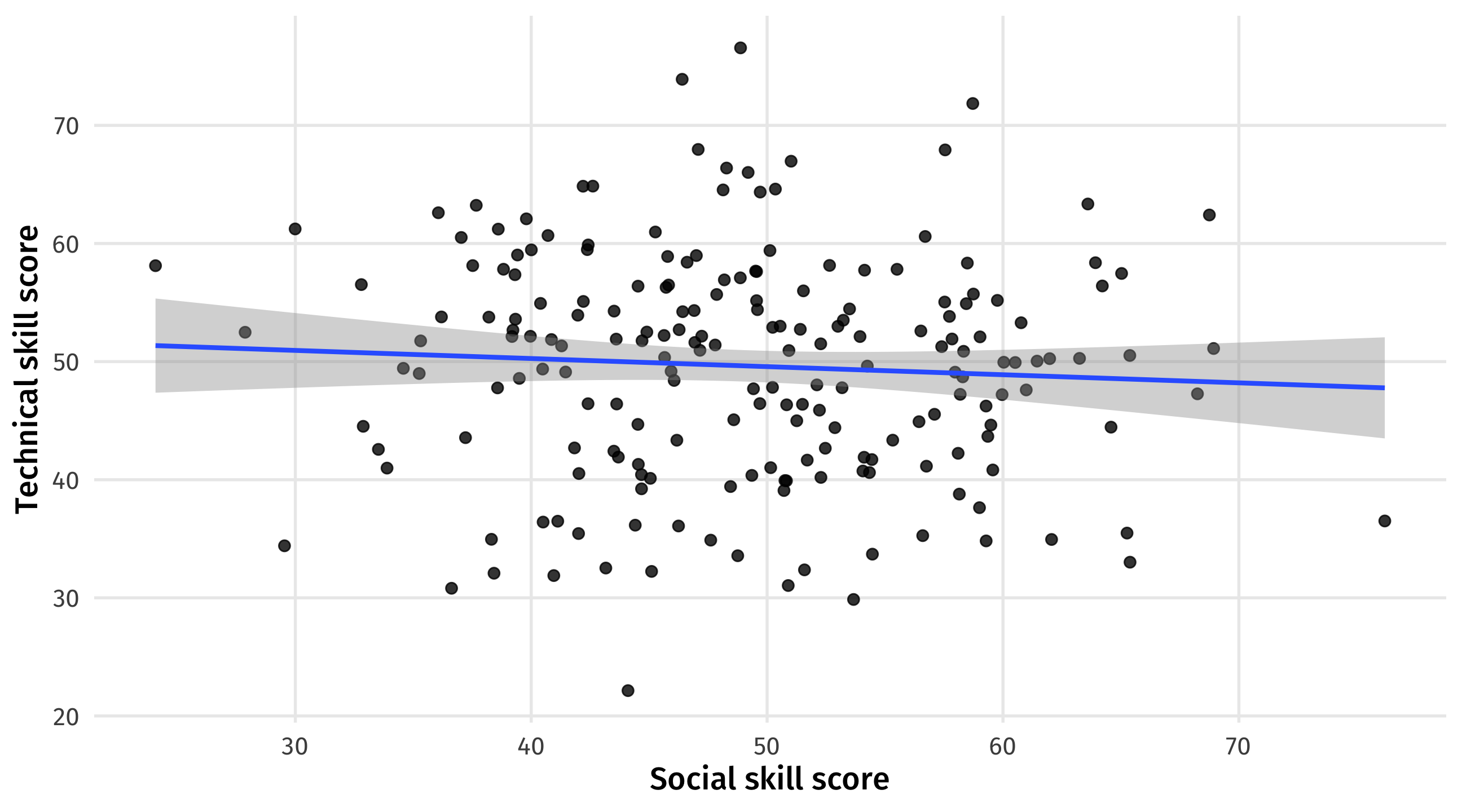
General population

No relationship between social and technical skills among all job candidates

Collided!

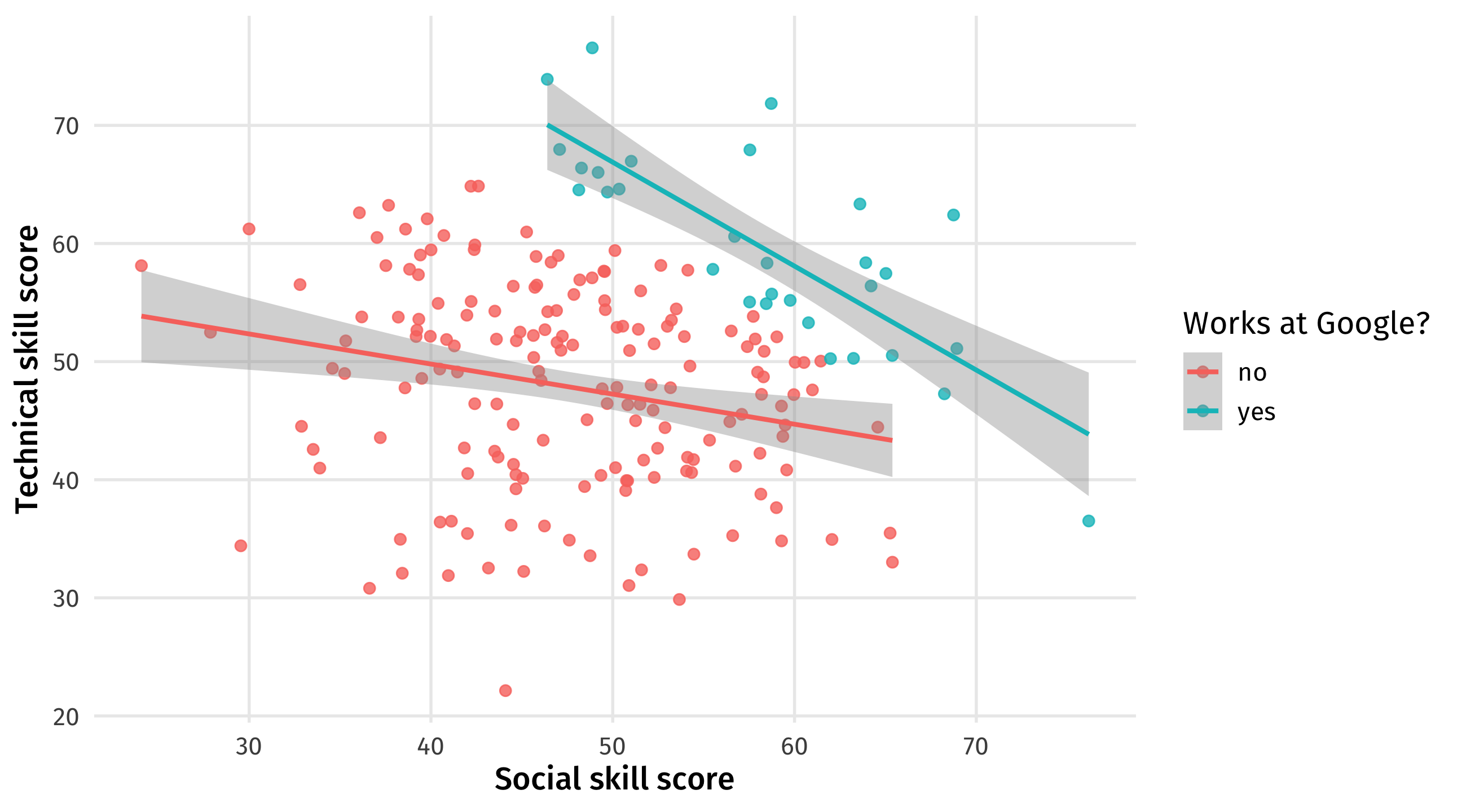
If we only look at Google workers we see a trade-off between social and technical skills:

Limitations

It’s cool that we can control for a confound, or avoid colliders/pipes and get back the truth

But there are big limitations we must keep in mind when evaluating research:

We need to know what to control for (confident in our DAG)

We need to have data on the controls (e.g., data on Z)

We need our data to measure the variable well (e.g., # of homicides a good proxy for crime?)

Stuff that’s hard to measure

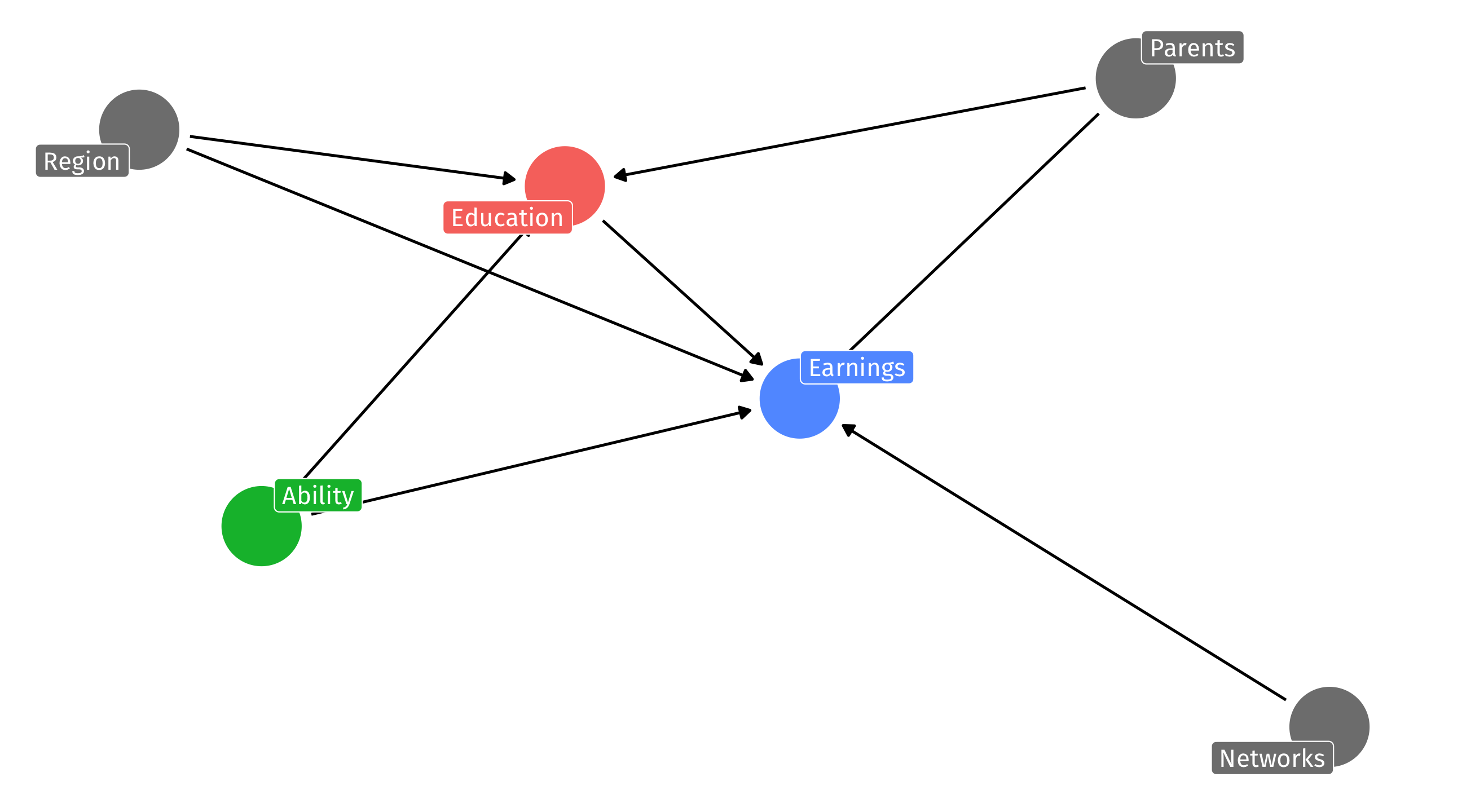
Ability is a likely fork for the effect of Education on Earnings; but how do you measure ability?

🚨 Your turn: pipes, colliders 🚨

Using the templates in the class script:

Make a realistic pipe scenario
Use models to show that everything goes wrong when you mistakenly control for the pipe
Make a realistic fork scenario
Use models to show that everything goes wrong when you fail to control for the fork

10:00