Modeling II

POL51

Juan Tellez

jftellez@ucdavis.edu

UC Davis

October 23, 2024

Plan for today

OLS in R

Modeling with continuous variables

Modeling with categorical variables

Uses of models

What we want out of our model:

• Does TV news make people more energized to vote? Or does it turn them off from politics?

• How much does an additional hour of TV increase (or decrease) the likelihood that someone votes?

• What level of Y (voter turnout) should we expect for a given level of X (exposure to the news)?

OLS in R

How does car weight impact fuel efficiency?

	mpg	cyl	disp	hp	drat	wt	qsec	vs	am	gear	carb
Valiant	18.1	6	225.0	105	2.8	3.5	20.2	1	0	3	1
Mazda RX4	21.0	6	160.0	110	3.9	2.6	16.5	0	1	4	4
Datsun 710	22.8	4	108.0	93	3.9	2.3	18.6	1	1	4	1
Duster 360	14.3	8	360.0	245	3.2	3.6	15.8	0	0	3	4
Mazda RX4 Wag	21.0	6	160.0	110	3.9	2.9	17.0	0	1	4	4
Merc 240D	24.4	4	146.7	62	3.7	3.2	20.0	1	0	4	2
Hornet 4 Drive	21.4	6	258.0	110	3.1	3.2	19.4	1	0	3	1

How does car weight impact fuel efficiency?

Remember, we want to estimate \(\beta_0\) (intercept) and \(\beta_1\) (slope)

\(mpg = \beta_0 + \beta1 \times weight\)

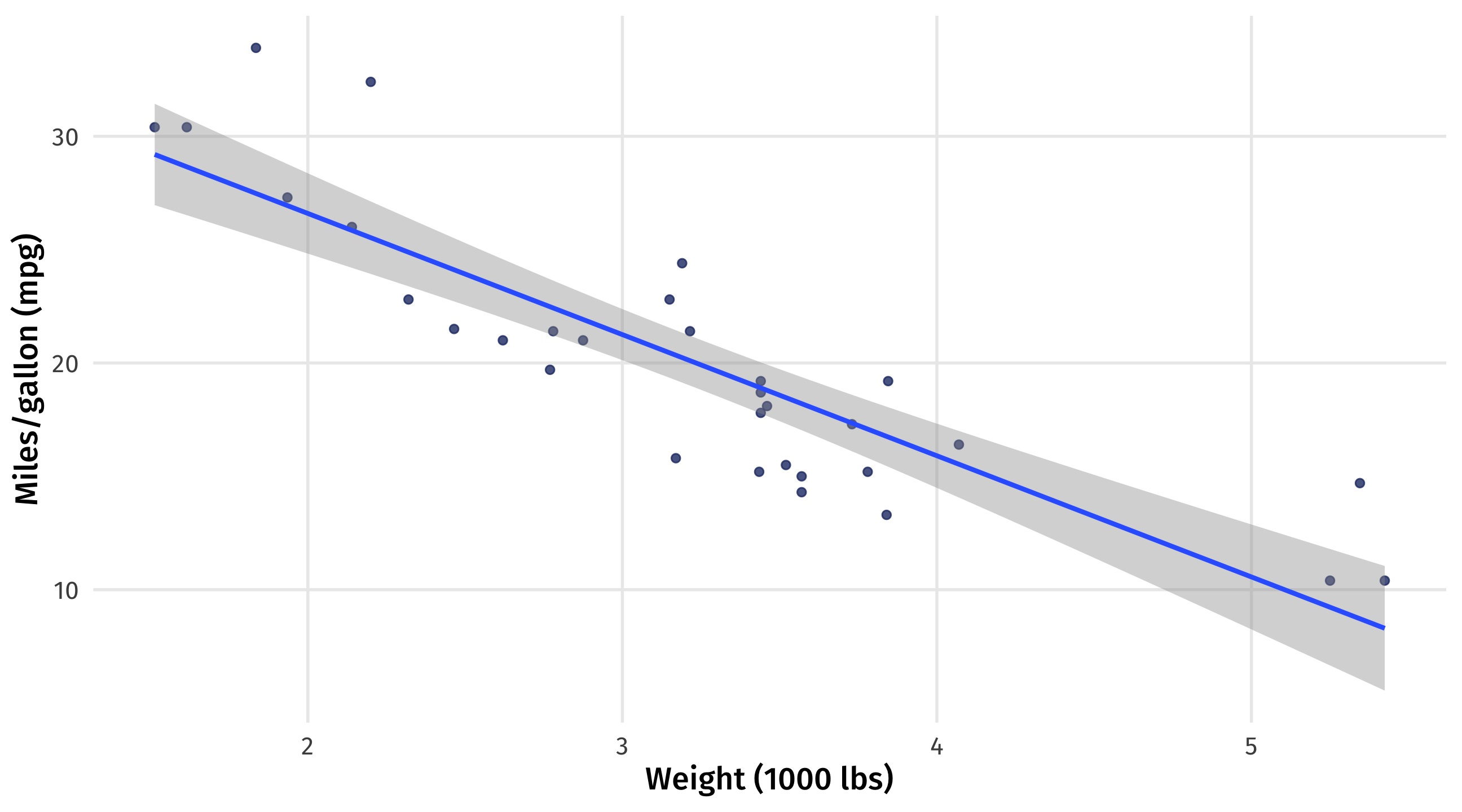
Fit the model

We can use lm() to fit models in R using this general formula:

lm(Outcome ~ X1 + X2 + …, data = DATA)

weight_model = lm(mpg ~ wt, data = mtcars)

Notice that I saved as an object, and the placement of the variables

The outcome always goes on the left hand side

The treatment variable goes on the right hand side

Extract the model

We can extract our estimates of \(\beta_0\) and \(\beta_1\) with tidy(), from the broom package

tidy(weight_model)

# A tibble: 2 × 5
  term        estimate std.error statistic  p.value
  <chr>          <dbl>     <dbl>     <dbl>    <dbl>
1 (Intercept)    37.3      1.88      19.9  8.24e-19
2 wt             -5.34     0.559     -9.56 1.29e-10

Note

You’ll need to load the broom package to use tidy() using library(broom)

Making sense of the table

\(mpg = \beta_0 + \beta_1 \times weight\)

tidy(weight_model)

# A tibble: 2 × 5
  term        estimate std.error statistic  p.value
  <chr>          <dbl>     <dbl>     <dbl>    <dbl>
1 (Intercept)    37.3      1.88      19.9  8.24e-19
2 wt             -5.34     0.559     -9.56 1.29e-10

The estimate column gives us \(\beta_0\) (intercept) and \(\beta_1\) (slope for weight)

Note! We only care about the first two columns of tidy() so far

Extract the model

\(mpg = \beta_0 + \beta_1 \times weight\)

term	estimate	std.error	statistic	p.value
(Intercept)	37.29	1.88	19.86	0
wt	-5.34	0.56	-9.56	0

The intercept ( \(\beta_0\) ) = 37.29

The slope ( \(\beta_1\) ) = -5.3

The model: \(mpg = 37.29 + -5.3 \times weight\)

Modeling with continuous variables

Back to the cars

The model: \(mpg = 37.29 + -5.3 \times weight\)

How do we interpret the slope on weight?

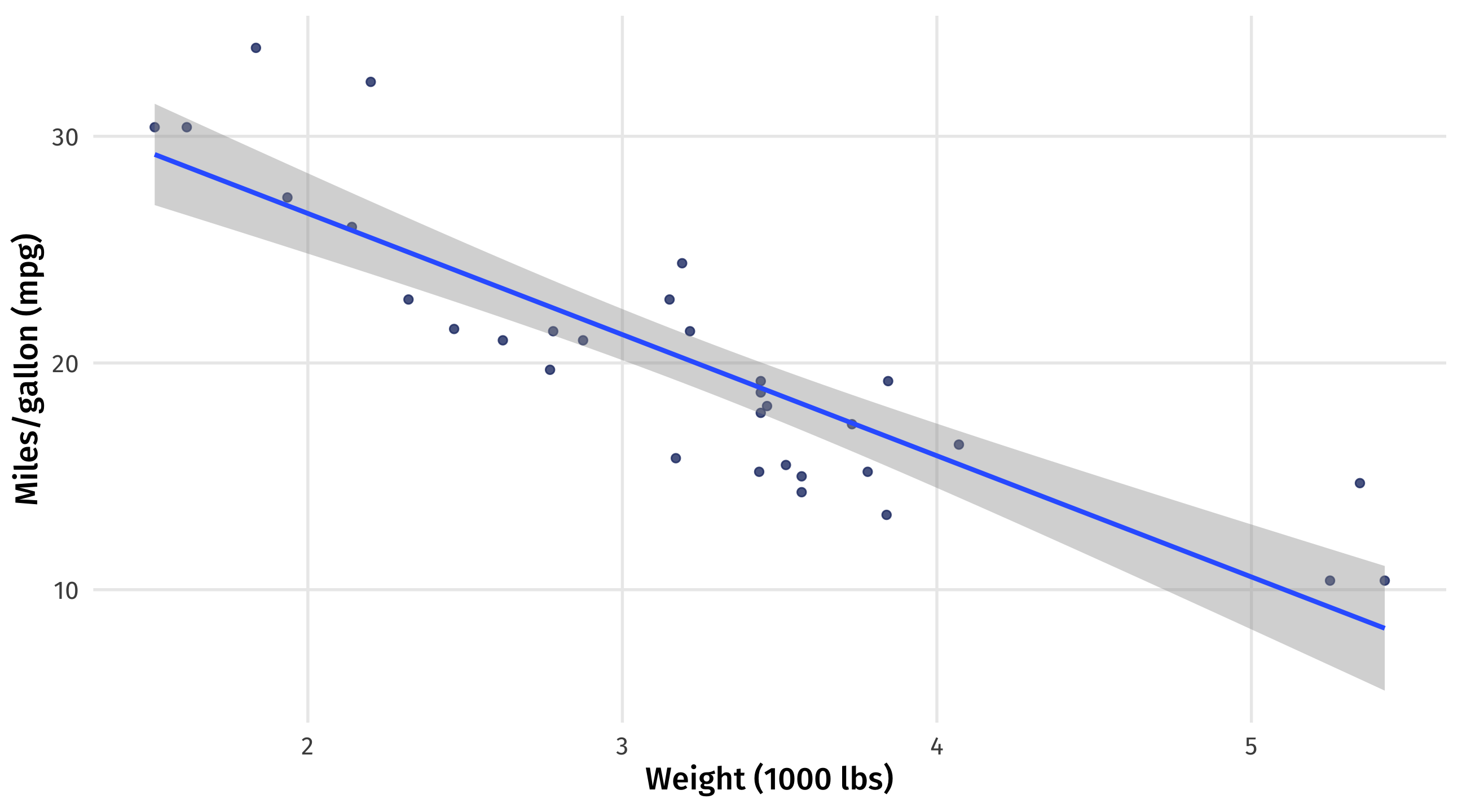
Interpretation: continuous variables

• As you turn the dimmer (treatment variable) the light (outcome variable) changes

• Turn the dimmer up, the light increases by SLOPE amount

• Turn the dimmer down, the light decreases by SLOPE amount

• The change is gradual

Interpretation: the slope

\(mpg = 37.2 + \color{red}{-5.3} \times weight\)

term	estimate	std.error	statistic	p.value
(Intercept)	37.29	1.88	19.86	0
wt	-5.34	0.56	-9.56	0

General: for every unit increase in X, Y changes by \(\color{red}{5.3}\) units

Specific: for every ton of weight you add to a car, you lose \(\color{red}{5.3}\) miles per gallon of fuel efficiency

Interpretation: the intercept

\(mpg = 37.2 + -5.3 \times weight\)

Remember that the Y-intercept is the value of Y when X = 0

\[ \begin{aligned} Y = 6 + 2x \\ X = 0 \\ Y = 6 + 2 \times 0 \\ Y = 6 \end{aligned} \]

Interpretation: the intercept

Take the formula: \(mpg = 37.2 + -5.3 \times weight\)

Set X (weight) equal to 0 \(\rightarrow\) \(\color{red}{37.2} + (-5.3 \times 0) = \color{red}{37.2}\)

General: The estimated value of Y, when X equals zero, is \(\color{red}{37.2}\) units

Specific: The estimated fuel efficiency for a car that weighs 0 tons is \(\color{red}{37.2}\) miles per gallon

Spot the intercept

\(mpg = 37.29 + -5.3 \times weight\)

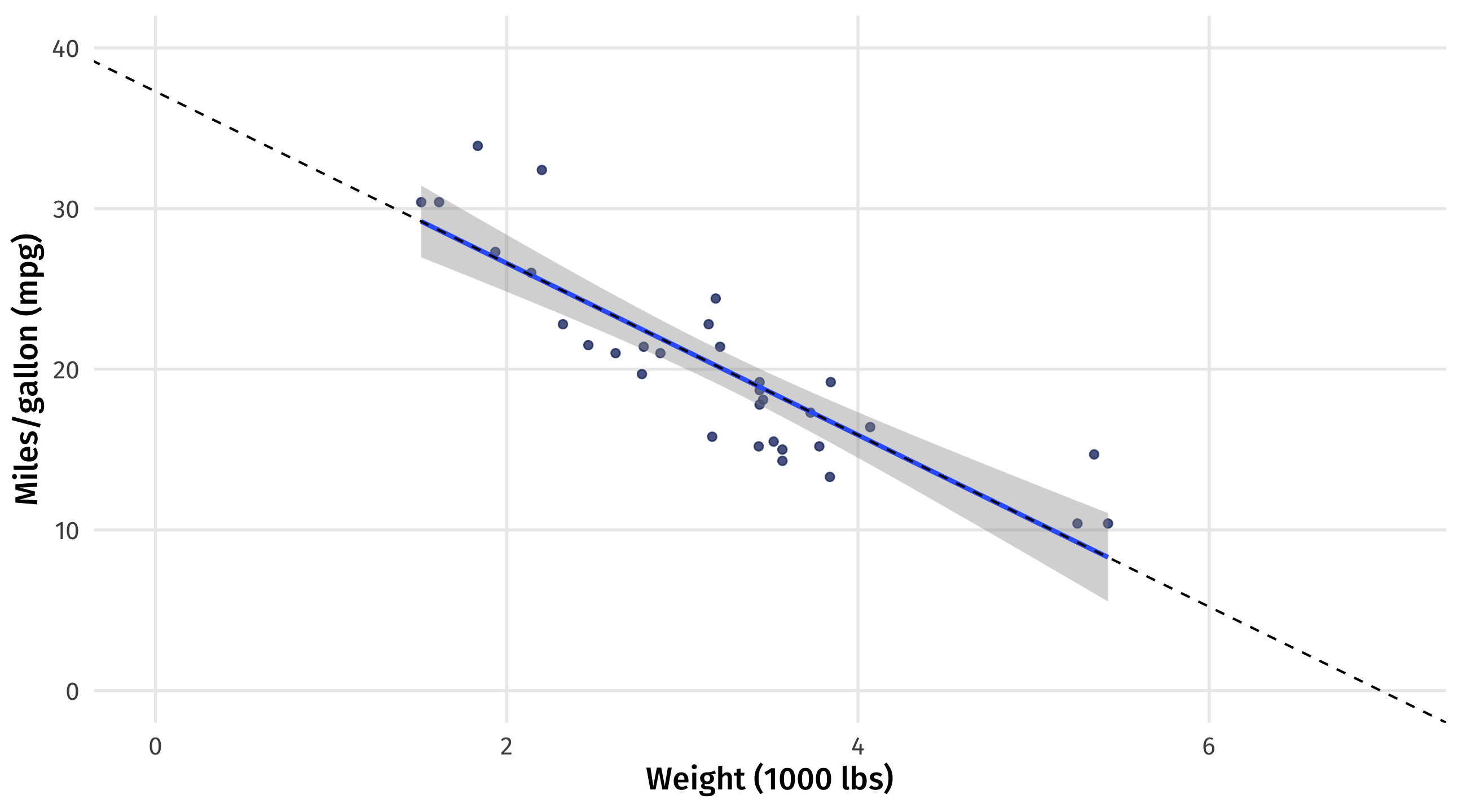
We can confirm we’re not crazy if we zoom out; the line crosses y-axis at 37.2

Nonsense intercepts

\(mpg = 37.2 + -5.3 \times weight\)

Interpretation of the intercept:

The average fuel efficiency for a car that weighs nothing is 37.2 miles per gallon

This is nonsense: a car cannot weigh zero tons

You will run into this often: don’t let it confuse you!

the intercept will rarely be useful on its own; But we need it to make predictions

Another example: gapminder

What’s the relationship between GDP per capita and life expectancy?

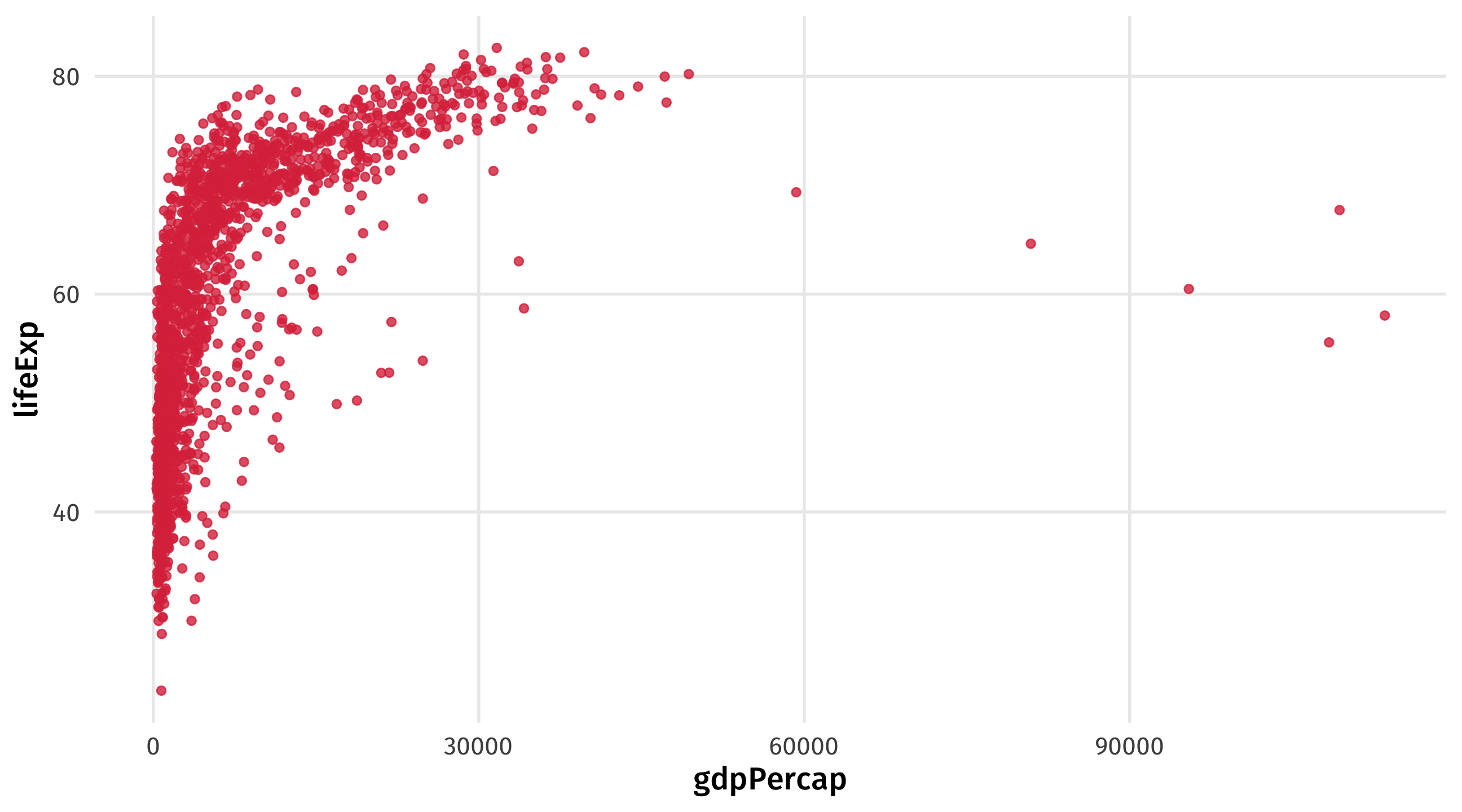
Another example: gapminder

What’s the relationship between GDP per capita and life expectancy?

country	continent	year	lifeExp	pop	gdpPercap
Paraguay	Americas	1997	69	5154123	4247
Sierra Leone	Africa	1962	33	2467895	1117
Eritrea	Africa	1982	44	2637297	525
Sao Tome and Principe	Africa	2002	64	170372	1353
Senegal	Africa	1982	52	6147783	1518

Notice the units: life expectancy in years, GDP in dollars per capita

The model

We fit the model using lm()

wealth_mod = lm(lifeExp ~ gdpPercap, data = gapminder)

We extract the coefficient estimates using tidy()

tidy(wealth_mod)

# A tibble: 2 × 5
  term         estimate std.error statistic   p.value
  <chr>           <dbl>     <dbl>     <dbl>     <dbl>
1 (Intercept) 54.0      0.315         171.  0        
2 gdpPercap    0.000765 0.0000258      29.7 3.57e-156

Interpreting the estimates

\(LifeExp = \beta_0 + \beta_1 \times gdpPercap\)

# A tibble: 2 × 5
  term         estimate std.error statistic   p.value
  <chr>           <dbl>     <dbl>     <dbl>     <dbl>
1 (Intercept) 54.0      0.315         171.  0        
2 gdpPercap    0.000765 0.0000258      29.7 3.57e-156

\(\beta_1\), the slope = for every additional dollar of GDP, a country’s life expectancy rises by .0007 years

\(\beta_0\), the intercept = the average life expectancy for a country with no economic activity (GDP = 0) is 54 years

The scale of the coefficients

\(LifeExp = 54 + .0007 \times gdpPercap\)

Slope: for every dollar increase in GDP, life expectancy increases by 0.0007 years

Tiny! Does this mean a country’s wealth has little to do with their health?

No! It is a problem with the scale that GDP is in (dollars!)

One dollar differences in GDP are tiny, meaningless

Mind your scales

Sample from gapminder

country	continent	year	lifeExp	pop	gdpPercap
Bolivia	Americas	1957	42	3211738	2128
Syria	Asia	1997	72	15081016	4014
Puerto Rico	Americas	1982	74	3279001	10331
Australia	Oceania	1957	70	9712569	10950

• one dollar increase = 0.0007 years increase in life expectancy
• one thousand dollar increase = 0.7 years increase in life expectancy
• ten thousand dollar increase = 7 years increase in life expectancy

🚨 🚢 Who trades? 🚢 🚨

Fit a model that estimates how much a country exports, using a treatment variable of your choosing. Interpret the model output.

05:00

Regression with categorical variables

Categorical variables

We can also use categorical variables in our models

The simplest categorical variable is a binary variable: Men vs. women, young vs. old, has a policy in place (vs. not), TRUE/FALSE

Organ donation

from socviz::organdata

country	year	donors	opt
United States	1994-01-01	19.4	In
Norway	1996-01-01	15.1	Out
United States	1996-01-01	20.1	In
Denmark	1995-01-01	12.9	In
Austria	2001-01-01	23.9	Out

Let’s look at data on the relationship between organ donation laws and how frequently people donate their organs

organ donation laws in this data are binary: in some countries, people have to opt out of donating their organs

In other countries, people have to opt in (like in the US)

Binary variables in models

I can include the binary variable in a regression model:

donor_mod = lm(donors ~ opt, data = organdata)

And look at the output:

# A tibble: 2 × 5
  term        estimate std.error statistic  p.value
  <chr>          <dbl>     <dbl>     <dbl>    <dbl>
1 (Intercept)    14.3      0.446     32.1  7.10e-76
2 optOut          5.50     0.705      7.80 5.00e-13

But how do we interpret the “slope” of a binary variable?

Binary variables

Remember, with categorical variables we are comparing groups

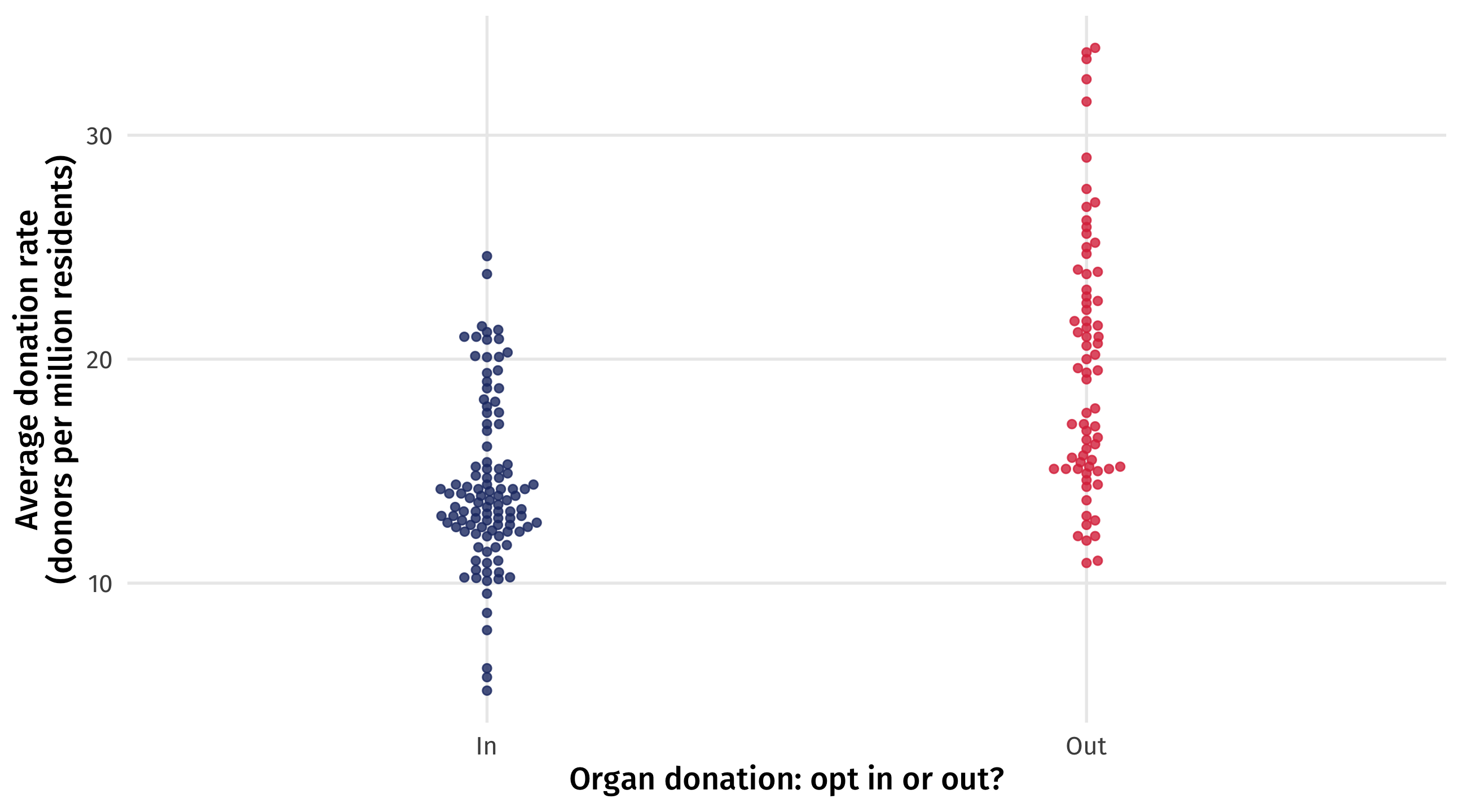
Binary variables: fitting the model

We can think about a line running “across” the groups, with each endpoint being optimally located to minimize the squared distances within each group

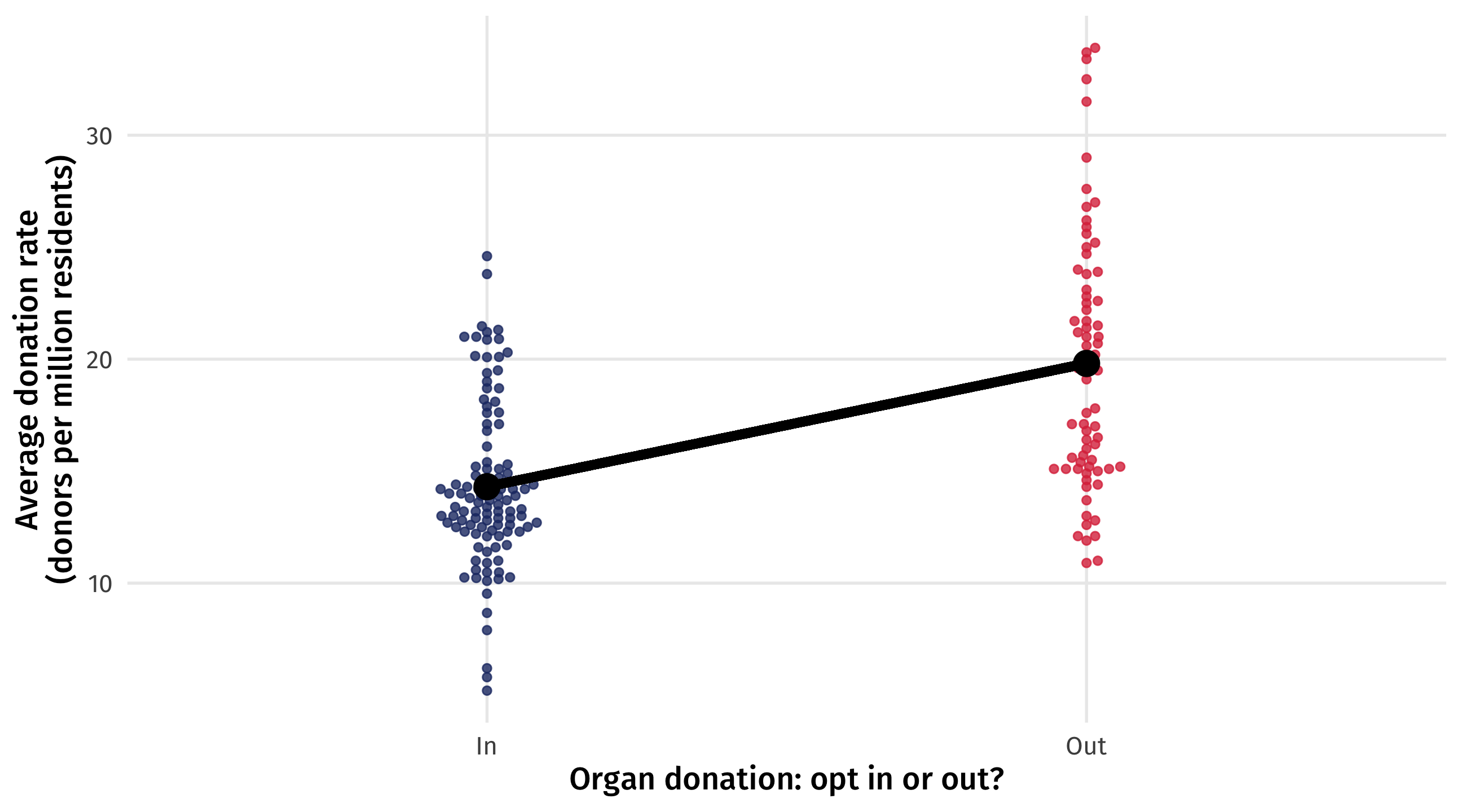
Binary variables: the slope

The height of one endpoint relative to the other, or the slope of the line, tells us how much higher or lower one group is, on average, than the other

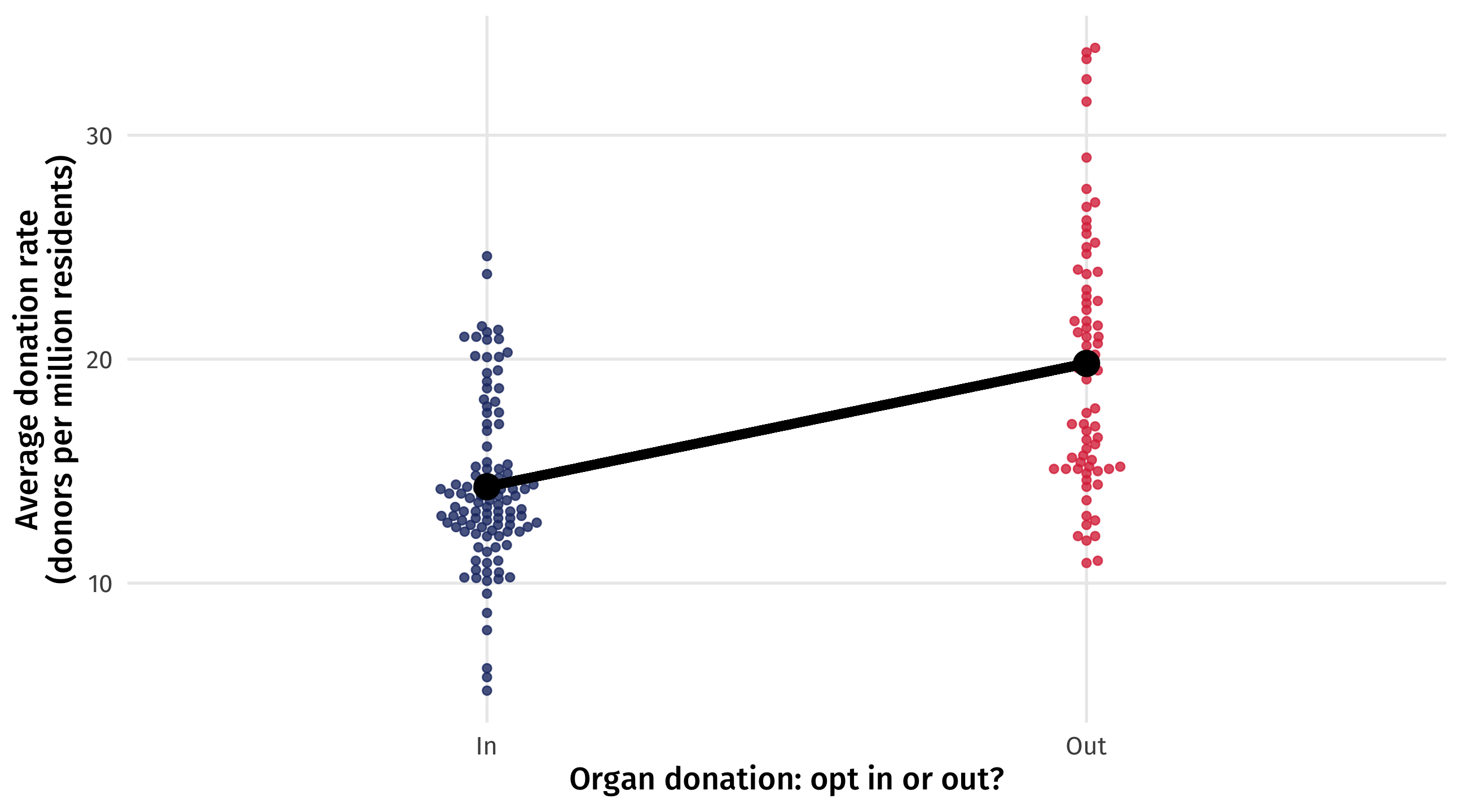
In this case it is 5.5 \(\rightarrow\) how many more organ donors countries with an “opt out” policy have, on average, than countries with an “opt in” policy

Back to the regression output

Note that this is exactly what the model output is giving us:

# A tibble: 2 × 5
  term        estimate std.error statistic  p.value
  <chr>          <dbl>     <dbl>     <dbl>    <dbl>
1 (Intercept)    14.3      0.446     32.1  7.10e-76
2 optOut          5.50     0.705      7.80 5.00e-13

The model is picking one of the categories (“Opt in”) and treating it as a baseline category

It tells us how much higher/lower on average, the other category is (“Opt out”)

How to interpret categorical variables?

• Turn the light on (opt goes from “In” to “Out”), the light increases by SLOPE

• Turn the light off (opt goes from “Out” to “In”), the light decreases by SLOPE

• The change is instant

Interpreting categories

\(\operatorname{\widehat{donors}} = \color{red}{14.31} + \color{blue}{5.5}(\operatorname{opt}_{\operatorname{Out}})\)

# A tibble: 2 × 5
  term        estimate std.error statistic  p.value
  <chr>          <dbl>     <dbl>     <dbl>    <dbl>
1 (Intercept)    14.3      0.446     32.1  7.10e-76
2 optOut          5.50     0.705      7.80 5.00e-13

Slope: Country-years where people have to OPT OUT of donating their organs have, on average, 5.5 more donations per million residents than country-years where people have to OPT IN

Intercept (set optOut = 0 or “off”, i.e., countries where opt == "in"):

Country-years where people have to OPT IN to organ donation have, on average, 14.31 donations per million residents

More complicated categorical variables

Most of the variables we care about are not just binary

They take on many values

E.g., education levels, sex, race, religion, etc.

What happens when we include one of these in a model?

Say we wanted to look at how being in a particular continent shapes a country’s life expectancy

The model

We can estimate the model, same as before:

continent_mod = lm(lifeExp ~ continent, data = gapminder)
tidy(continent_mod)

# A tibble: 5 × 5
  term              estimate std.error statistic   p.value
  <chr>                <dbl>     <dbl>     <dbl>     <dbl>
1 (Intercept)           48.9     0.370     132.  0        
2 continentAmericas     15.8     0.649      24.3 1.38e-112
3 continentAsia         11.2     0.593      18.9 2.44e- 72
4 continentEurope       23.0     0.611      37.7 1.38e-226
5 continentOceania      25.5     1.92       13.3 2.99e- 38

Now we get more coefficients! What do they mean?

Look at the data

With complex categorical variables, we are also comparing across groups

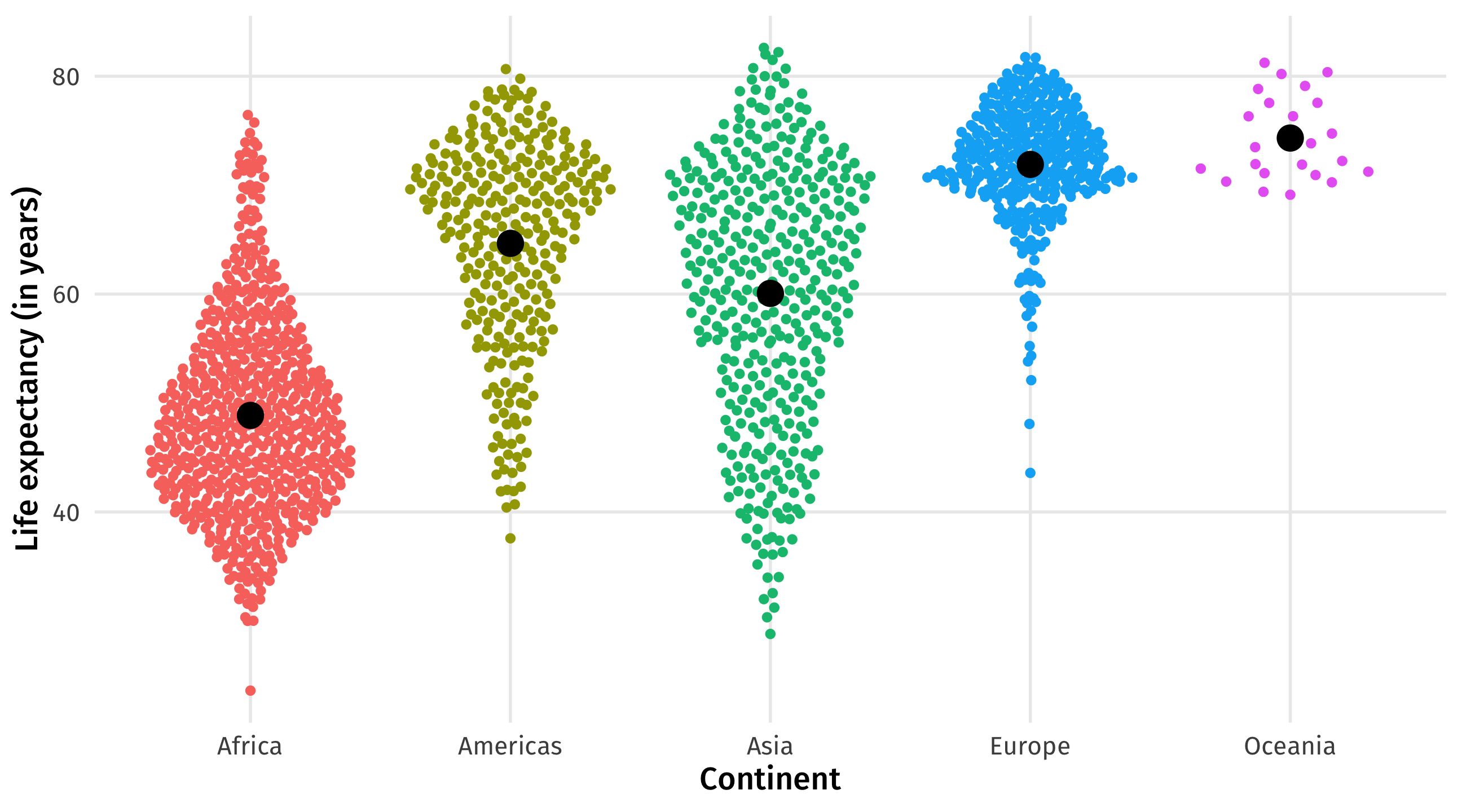
We can also identify the value within each group that minimizes \((Y_i - \hat{Y_i})^2\)

But how to draw a “line” across all these groups?

Multiple categories

Just like before, R will pick one of the groups to treat as the “baseline”

It will then tell us how much higher/lower the other categories are, on average, relative to that baseline category

# A tibble: 5 × 5
  term              estimate std.error statistic   p.value
  <chr>                <dbl>     <dbl>     <dbl>     <dbl>
1 (Intercept)           48.9     0.370     132.  0        
2 continentAmericas     15.8     0.649      24.3 1.38e-112
3 continentAsia         11.2     0.593      18.9 2.44e- 72
4 continentEurope       23.0     0.611      37.7 1.38e-226
5 continentOceania      25.5     1.92       13.3 2.99e- 38

What group is the baseline here?

Interpretation

# A tibble: 5 × 5
  term              estimate std.error statistic   p.value
  <chr>                <dbl>     <dbl>     <dbl>     <dbl>
1 (Intercept)           48.9     0.370     132.  0        
2 continentAmericas     15.8     0.649      24.3 1.38e-112
3 continentAsia         11.2     0.593      18.9 2.44e- 72
4 continentEurope       23.0     0.611      37.7 1.38e-226
5 continentOceania      25.5     1.92       13.3 2.99e- 38

• continentAmericas = countries in the Americas have, on average, 15.8 years more life expectancy than countries in Africa (the baseline)

• continentAsia = countries in Asia have, on average, 11.2 years more life expectancy than countries in Africa

• Intercept = (set Americas = 0, Asia = 0, Europe = 0, Oceania = 0) \(\rightarrow\) the average life expectancy in Africa is 48.9 years

Interpretation formula

Type	Approach	Intercept
Continuous	A one unit increase in X, SLOPE unit change in Y	Average value of Y when X = 0
Category	The category is SLOPE units higher/lower than the intercept	Average value of Y for baseline (missing) category

Interpreting coefficients is pretty confusing; it just requires practice

We’re on our way

We now know (sort of) how to interpret the coefficients on those big tables:

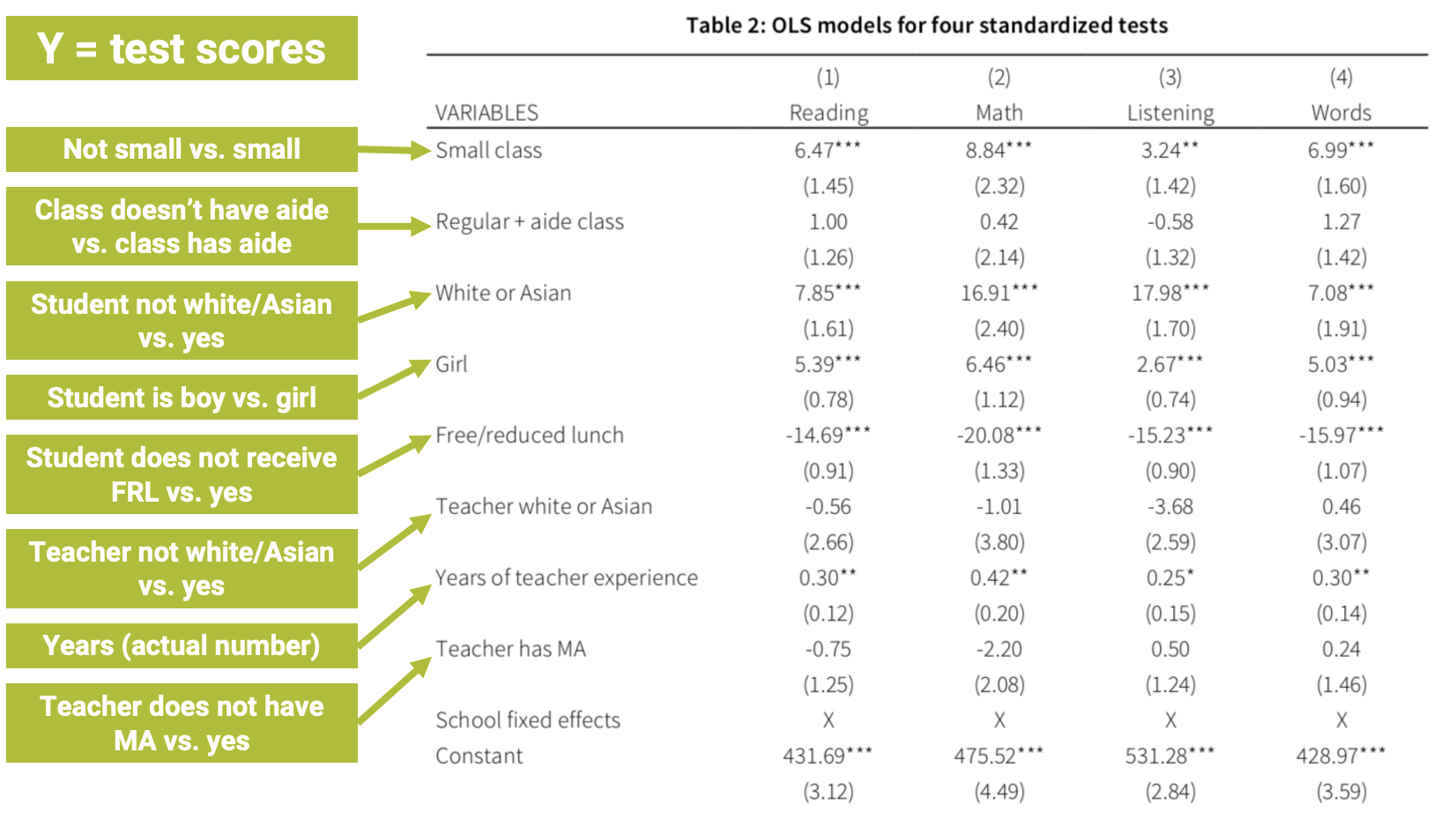
🚨 Your turn: 👨‍👧‍👦 Kids 👨‍👧‍👦 🚨

Using the gss_sm dataset:

1. Do happier people tend to have more or fewer kids than less happy people? Regress childs (outcome) against happy (treatment). Interpret the output.

2. How does religion affect family size? Regress the number of siblings sibs (outcome) against respondent religion relig. Based on the output: which religion has the largest families, on average?

Note

Remember: to figure out what values a categorical variable takes on, use the distinct() function, like so: data %>% distinct(variable)

10:00