Relationships II

POL51

Juan Tellez

jftellez@ucdavis.edu

UC Davis

October 16, 2024

Get ready

Boot up Posit Cloud
Download the script for today’s examples
- Schedule ➡️ Example ➡️ Today
Upload the script to Posit Cloud

Plan for today

Comparing across groups

Dummy variables

Summarizing categories

🌡️ ugly prejudice 🌡️ 🚨

Researchers use feeling thermometers to measure how people feel about different groups

🌡 goes from zero (strong dislike) to 100 (strong like)

🌡️ ugly prejudice 🌡️ 🚨

Sample of respondents from {therm}.
birth_year	sex	race	party_id	educ	ft_black	ft_white	ft_hisp	ft_asian	ft_muslim	ft_jew	ft_christ	ft_fem	ft_immig	ft_gays	ft_unions	ft_police	ft_altright	ft_evang	ft_dem	ft_rep
1931	Female	White	Democrat	4-year	51	50	79	50	50	50	50	99	95	50	80	76	1	50	88	21
1952	Female	White	Republican	2-year	98	90	95	100	61	100	98	65	96	82	62	95	50	96	86	96
1931	Male	White	Independent	High school graduate	87	90	91	88	49	25	50	74	77	77	100	78	0	2	91	20
1952	Male	White	Republican	4-year	90	85	90	96	80	91	94	25	91	71	20	94	50	70	22	83
1939	Female	White	Democrat	2-year	100	50	100	100	100	100	28	100	100	100	100	28	NA	NA	99	NA
1959	Female	Black	Democrat	Post-grad	98	70	99	100	100	100	100	73	100	54	80	24	4	53	53	4

How do Americans feel about…

The police?

therm |> 
  summarise(avg_police = mean(ft_police, na.rm = TRUE))

# A tibble: 1 × 1
  avg_police
       <dbl>
1       75.7

Unions?

therm |> 
  summarise(avg_unions = mean(ft_unions, na.rm = TRUE))

# A tibble: 1 × 1
  avg_unions
       <dbl>
1       53.4

Making comparisons

We can compare which groups are viewed more (or less) favorably:

therm %>% 
  summarise(avg_police = mean(ft_police, na.rm = TRUE), 
            avg_muslim = mean(ft_muslim, na.rm = TRUE), 
            avg_white = mean(ft_white, na.rm = TRUE), 
            avg_immig = mean(ft_immig, na.rm = TRUE), 
            avg_fem = mean(ft_fem, na.rm = TRUE), 
            avg_black = mean(ft_black, na.rm = TRUE))

# A tibble: 1 × 6
  avg_police avg_muslim avg_white avg_immig avg_fem avg_black
       <dbl>      <dbl>     <dbl>     <dbl>   <dbl>     <dbl>
1       75.7       50.0      76.1      61.9    52.1      71.3

The partisan breakdown

We can look for patterns by using group_by() to separate average support by respondent characteristics:

How do partisans feel about each group?

therm %>% 
  # grouped summaries
  group_by(party_id) %>% 
  summarise(avg_police = mean(ft_police, na.rm = TRUE), 
            avg_muslim = mean(ft_muslim, na.rm = TRUE), 
            avg_white = mean(ft_white, na.rm = TRUE), 
            avg_immig = mean(ft_immig, na.rm = TRUE), 
            avg_fem = mean(ft_fem, na.rm = TRUE), 
            avg_black = mean(ft_black, na.rm = TRUE))

# A tibble: 5 × 7
  party_id    avg_police avg_muslim avg_white avg_immig avg_fem avg_black
  <fct>            <dbl>      <dbl>     <dbl>     <dbl>   <dbl>     <dbl>
1 Democrat          67.8       64.6      74.1      71.7    73.9      78.3
2 Republican        87.6       33.3      81.7      50.2    30.3      65.6
3 Independent       74.2       49.0      74.1      61.5    48.3      69.1
4 Other             72.7       45.1      71.1      65.4    40.7      70.2
5 Not sure          70.1       47.1      70.8      56.9    54.0      66.7

Breaking down support

We can use filter() to focus our comparison on fewer party ID categories:

therm_by_party = therm %>% 
  # look only at Democrats and Republicans
  filter(party_id == "Democrat" | party_id == "Republican") %>% 
  # grouped summaries
  group_by(party_id) %>% 
  summarise(avg_police = mean(ft_police, na.rm = TRUE), 
            avg_muslim = mean(ft_muslim, na.rm = TRUE), 
            avg_white = mean(ft_white, na.rm = TRUE), 
            avg_immig = mean(ft_immig, na.rm = TRUE), 
            avg_fem = mean(ft_fem, na.rm = TRUE), 
            avg_black = mean(ft_black, na.rm = TRUE))
therm_by_party

# A tibble: 2 × 7
  party_id   avg_police avg_muslim avg_white avg_immig avg_fem avg_black
  <fct>           <dbl>      <dbl>     <dbl>     <dbl>   <dbl>     <dbl>
1 Democrat         67.8       64.6      74.1      71.7    73.9      78.3
2 Republican       87.6       33.3      81.7      50.2    30.3      65.6

The immigration gap

What explains this gap? How much is it about each party’s ideology and how much is about who is in each party?

Immigrants in the USA are more likely to identify as Democrat

Could it be that the big gap we see is all because immigrants are both more likely to be Democrats and have more positive views of own community?

One test: compare non-migrants in each party to see if the gap persists

Making sense of the immigration gap

We want an apples to apples comparison: White Dems vs. White Reps, Asian Dems vs. Asian Reps, and so on

We can “test” this concern by breaking the data down further, by race:

therm %>% 
  filter(party_id == "Democrat" | party_id == "Republican") %>% 
  group_by(party_id, race) %>%
  summarise(avg_imm = mean(ft_immig, na.rm = TRUE))

# A tibble: 14 × 3
# Groups:   party_id [2]
   party_id   race            avg_imm
   <fct>      <fct>             <dbl>
 1 Democrat   White              71.2
 2 Democrat   Black              71.1
 3 Democrat   Hispanic           76.2
 4 Democrat   Asian              75.5
 5 Democrat   Native American    62.9
 6 Democrat   Mixed              74.6
 7 Democrat   Other              84.1
 8 Republican White              49.8
 9 Republican Black              54.6
10 Republican Hispanic           58.0
11 Republican Asian              54.7
12 Republican Native American    47.4
13 Republican Mixed              51.4
14 Republican Other              42.3

Making sense of the immigration gap

We can filter to focus on fewer races:

therm %>% 
  filter(party_id == "Democrat" | party_id == "Republican") %>% 
  filter(race %in% c("White", "Black", "Hispanic", "Asian")) |> 
  group_by(party_id, race) %>%
  summarise(avg_imm = mean(ft_immig, na.rm = TRUE))

# A tibble: 8 × 3
# Groups:   party_id [2]
  party_id   race     avg_imm
  <fct>      <fct>      <dbl>
1 Democrat   White       71.2
2 Democrat   Black       71.1
3 Democrat   Hispanic    76.2
4 Democrat   Asian       75.5
5 Republican White       49.8
6 Republican Black       54.6
7 Republican Hispanic    58.0
8 Republican Asian       54.7

Visualizing the pattern

We can create a new object to make a nice plot:

therm_party_immig = therm %>% 
  filter(party_id == "Democrat" | party_id == "Republican") %>% 
  filter(race %in% c("White", "Black", "Hispanic", "Asian")) |> 
  group_by(party_id, race) %>%
  summarise(avg_imm = mean(ft_immig, na.rm = TRUE))

The immigration attitudes gap

Code

ggplot(therm_party_immig, aes(y = avg_imm, 
                              x = race, fill = party_id)) + 
  geom_col(position = "dodge") + 
  labs(x = "Respondent race", y = "Average thermometer level\nfor immigrants", 
       fill = "Respondent race:") + 
  theme(legend.position = "none") + 
  geom_label(aes(label = party_id), position = position_dodge(1), color = "white") + 
  scale_fill_manual(values = c(blue, red))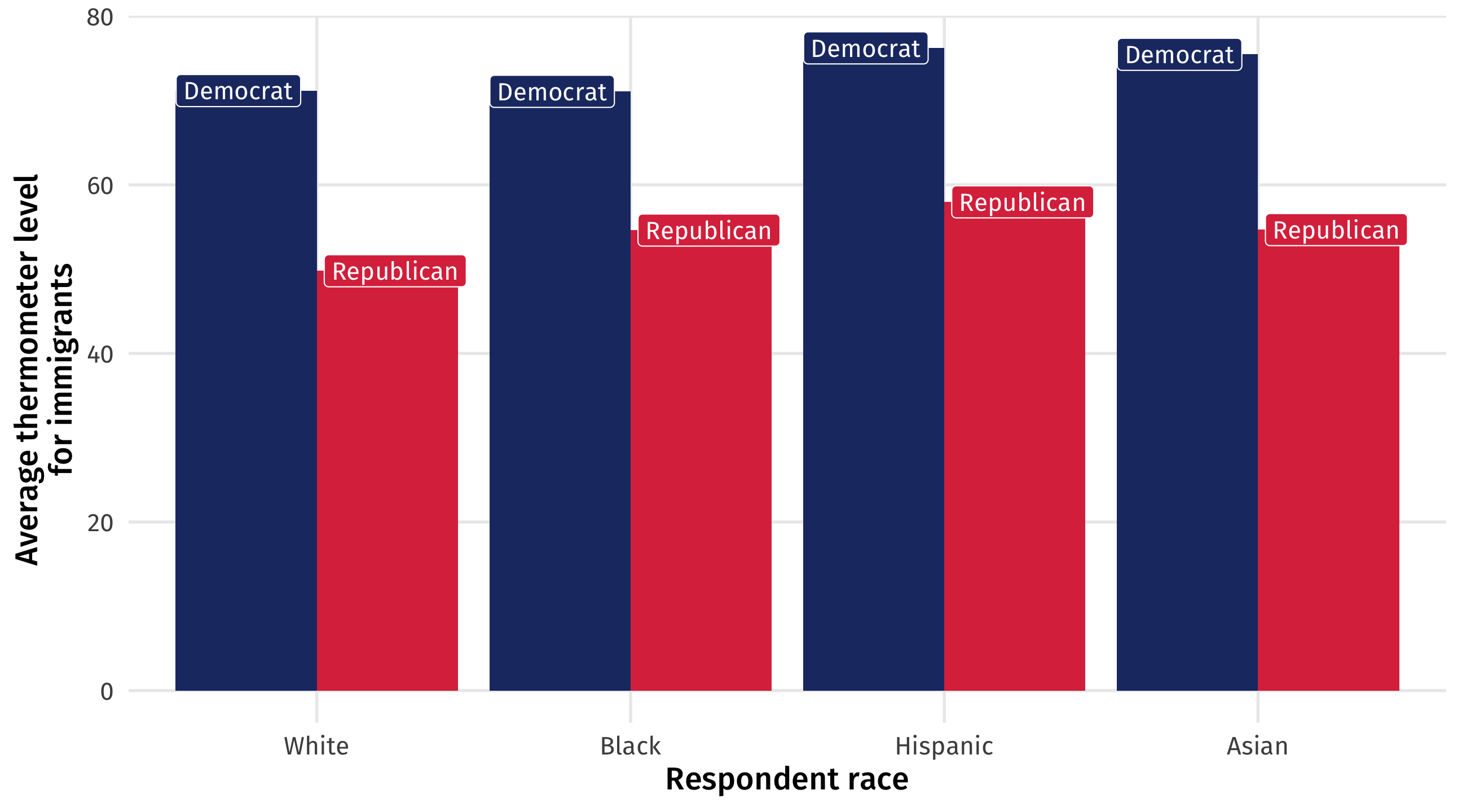

Big picture

The immigration gap persists (though smaller), even comparing non-immigrants against non-immigrants and immigrants against immigrants

This analysis is a way of accounting for differences in groups (Democrats versus Republicans); it’s closer to an “apples to apples” comparison

Big differences across groups should raise eyebrows; what’s going on here?

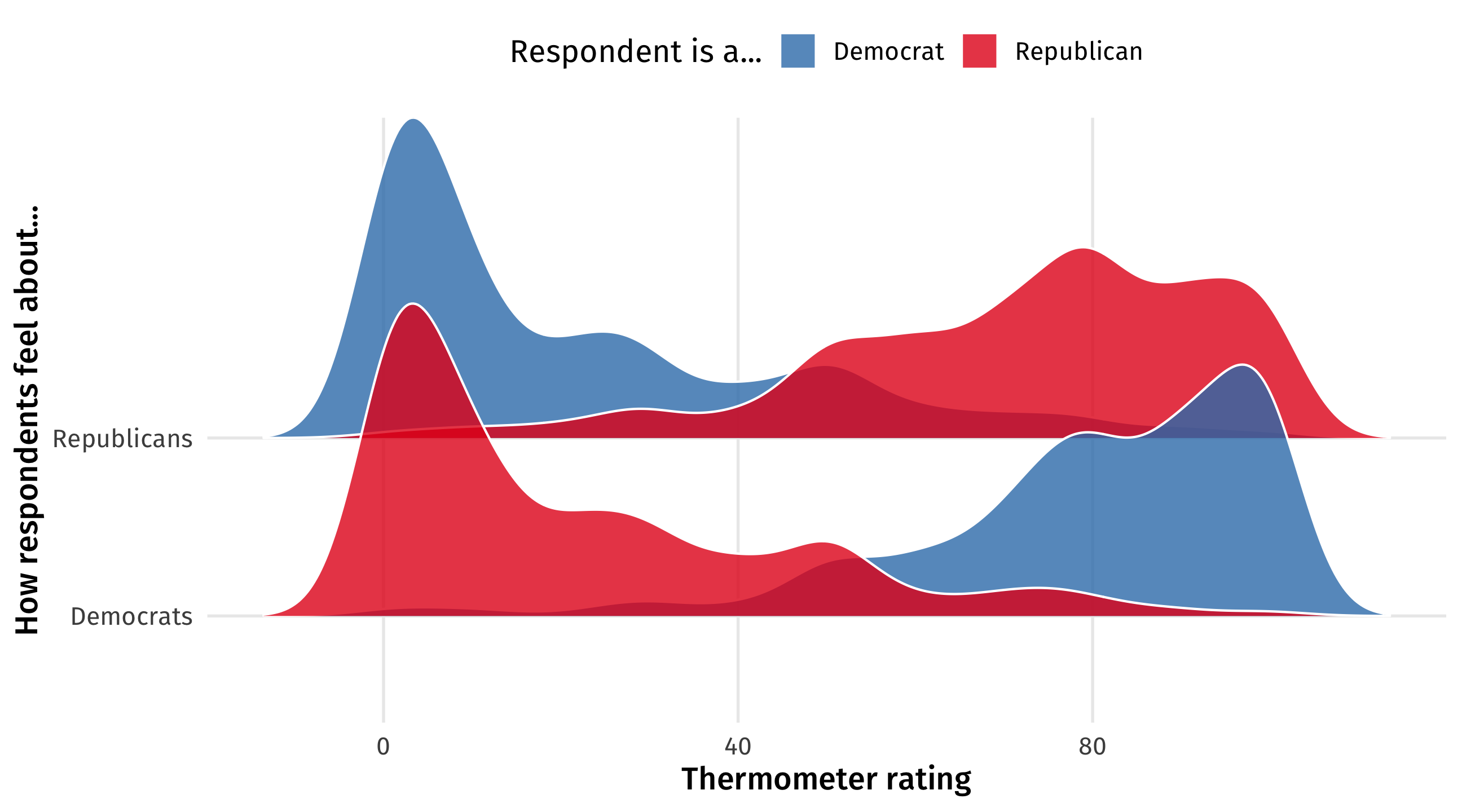
Non-differences can be surprsing too

therm %>% 
  summarise(avg_dems = mean(ft_dem, na.rm = TRUE), 
            avg_reps = mean(ft_rep, na.rm = TRUE))

# A tibble: 1 × 2
  avg_dems avg_reps
     <dbl>    <dbl>
1     49.4     43.3

Pretty neutral feelings; mass polarization is dead!

Oh…

Breaking down data says something different

therm %>% 
  group_by(party_id) %>%
  summarise(dems = mean(ft_dem, na.rm = TRUE), 
            reps = mean(ft_rep, na.rm = TRUE))

# A tibble: 5 × 3
  party_id     dems  reps
  <fct>       <dbl> <dbl>
1 Democrat     79.9  22.1
2 Republican   21.5  72.4
3 Independent  41.2  39.6
4 Other        31.9  38.7
5 Not sure     43.2  42.3

Negative polarization

Dummy variables

Often, categorical variables are coded 0/1 to represent “yes/no” or “presence/absence”

sample from leaders dataset
country	leader	mil_service	combat
NEW	Holland	1	1
LEB	Elias Hrawi	0	0
PER	Benavides	1	1
IRE	Haughey	0	0
BOT	Ian Khama	NA	NA

mil_service is a dummy variable: 1 if leader has military service, 0 otherwise; combat is the same but for combat experience

Dummy proportions

Dummy variables are useful for lots of reasons

One is that when you take the average of a dummy variable you get a proportion

Coffee today? 1, 0, 0, 0, 1

Average of coffee = $\frac{1 + 0 + 0 + 0 + 1}{5} = .40$

We can think about that proportion as a probability or likelihood

What is the probability a random student in class has had coffee? 2/5 = 40%

Dummy variables

When you take the average of a dummy variable you get a proportion:

leader %>% 
  summarise(combat = mean(combat, na.rm = TRUE))

# A tibble: 1 × 1
  combat
   <dbl>
1  0.246

Approximately 24% of world leaders have combat experience, or

there’s a 24% chance a randomly selected leader has combat experience

Dummy variables

Like with anything else, we can take averages by groups

For example, combat experience by country

leader %>% 
  group_by(country) %>%
  summarise(combat = mean(combat, na.rm = TRUE))

# A tibble: 189 × 2
   country combat
   <chr>    <dbl>
 1 AFG      0.479
 2 ALB      0.255
 3 ALG      0.403
 4 ANG      0    
 5 ARG      0.362
 6 ARM      0    
 7 AUH      0.958
 8 AUL      0.110
 9 AUS      0.234
10 AZE      0    
# ℹ 179 more rows

Dummy variables

We can store as an object, to make a plot:

Code

combat_country = leader %>% 
  group_by(country) %>%
  # proportion who've seen combat
  summarise(combat = mean(combat, na.rm = TRUE)) |> 
  # subset to just the top 10 in terms of combat experience
  slice_max(order_by = combat, n = 10)

ggplot(combat_country, aes(y = reorder(country, combat),
                           x = combat)) + 
  geom_col(fill = "#213772") + 
  labs(x = "Proportion of leaders with combat experience", 
       y = "Country", title = "Top 10 countries with leaders who have seen combat")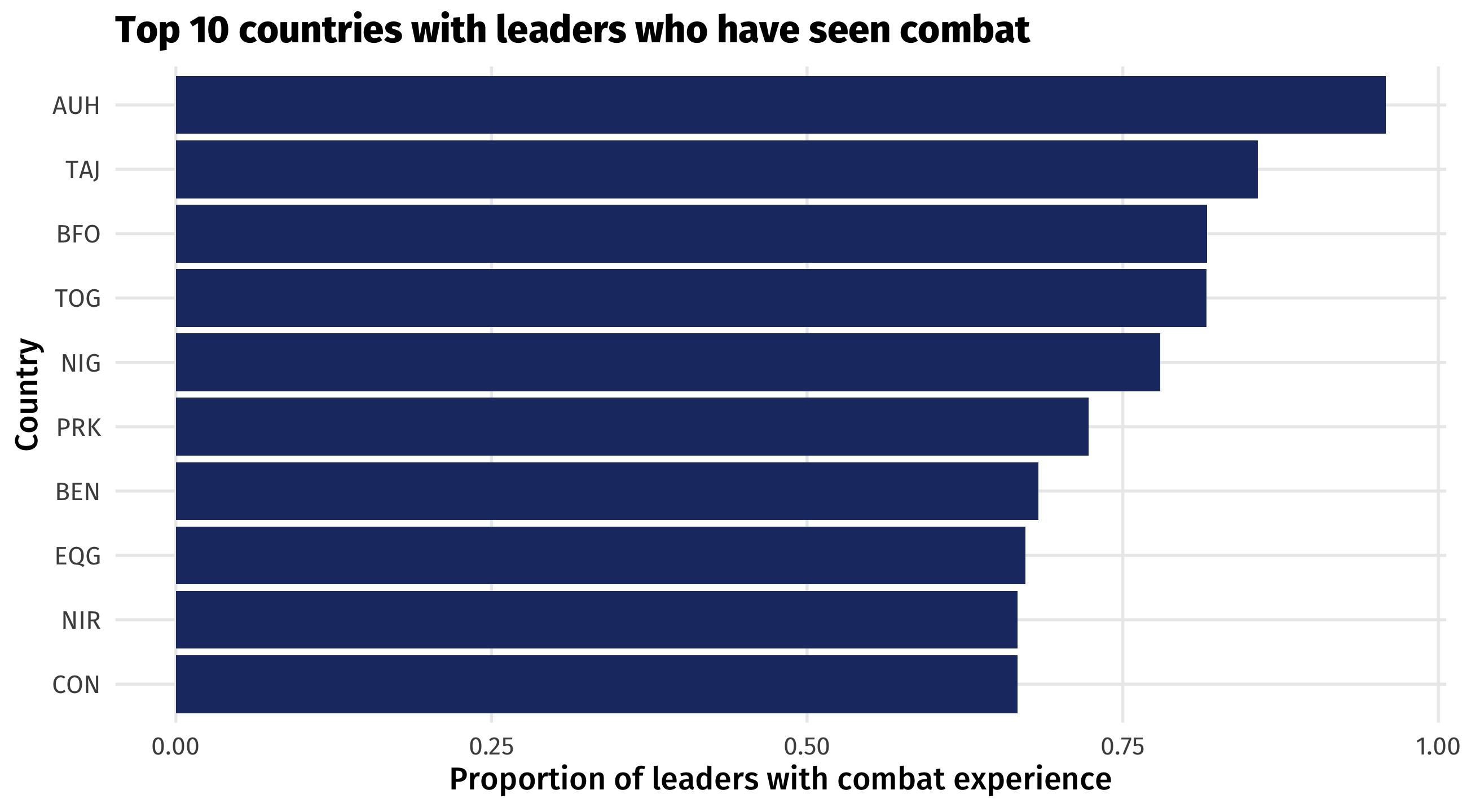

🚨 Your turn: 🎨 Bob Ross 🎨 🚨

episode	season	episode_num	title	bushes	cabin	clouds	conifer	deciduous	fence	grass	lake	moon	mountain	mountains	night	river	rocks	snow	snowy_mountain	structure	sun	tree	trees	winter
S01E01	1	1	A WALK IN THE WOODS	1	0	0	0	1	0	1	0	0	0	0	0	1	0	0	0	0	0	1	1	0
S01E02	1	2	MT. MCKINLEY	0	1	1	1	0	0	0	0	0	1	0	0	0	0	1	1	0	0	1	1	1
S01E03	1	3	EBONY SUNSET	0	1	0	1	0	1	0	0	0	1	1	0	0	0	0	0	1	1	1	1	1
S01E04	1	4	WINTER MIST	1	0	1	1	0	0	0	1	0	1	0	0	0	0	0	1	0	0	1	1	0
S01E05	1	5	QUIET STREAM	0	0	0	0	1	0	0	0	0	0	0	0	1	1	0	0	0	0	1	1	0
S01E06	1	6	WINTER MOON	0	1	0	1	0	0	0	1	1	1	1	1	0	0	1	1	1	0	1	1	1

🚨 Your turn: 🎨 Bob Ross 🎨 🚨

Using the bob_ross data from fivethirtyeight package

How likely was Bob Ross to include a happy little tree in one of his paintings?
How has the frequency with which Bob Ross included clouds in his paintings changed across the show’s seasons? Make a time series to illustrate.
If there is a mountain in a Bob Ross painting, how likely is it that mountain is snowy (snowy_mountain)?
How much more likely was Steve Ross (steve) to paint a lake (lake) than his dad?

10:00

Analyzing categorical data

Some variables have values that are categories (race, sex, etc.)

Can’t take the mean of a category!

But we can look at the proportions of observations in each category, and look for patterns there

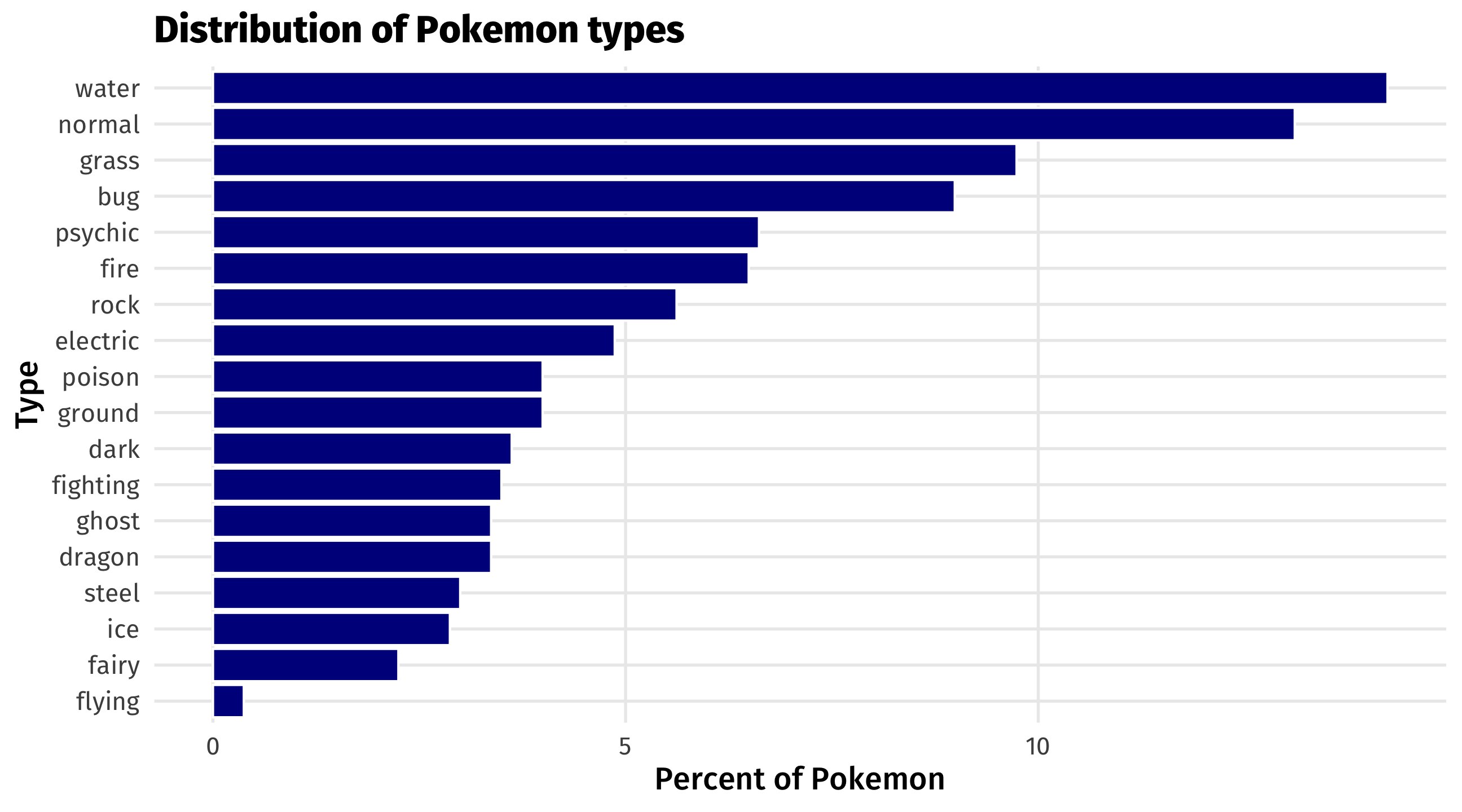
Pokemon types

How many Pokemon are there of each type? What are the most and least common types?

name	type1
Aipom	normal
Claydol	ground
Litwick	ghost
Ninetales	fire
Sawk	fighting
Hitmonchan	fighting
Scizor	bug

Counting categories

We can use a new function count(), to count how many observations are in each category:

pokemon

# A tibble: 801 × 14
   name       type1 type2  height_m weight_kg capture_rate    hp attack defense
   <chr>      <chr> <chr>     <dbl>     <dbl>        <dbl> <dbl>  <dbl>   <dbl>
 1 Bulbasaur  grass poison      0.7       6.9           45    45     49      49
 2 Ivysaur    grass poison      1        13             45    60     62      63
 3 Venusaur   grass poison      2       100             45    80    100     123
 4 Charmander fire  <NA>        0.6       8.5           45    39     52      43
 5 Charmeleon fire  <NA>        1.1      19             45    58     64      58
 6 Charizard  fire  flying      1.7      90.5           45    78    104      78
 7 Squirtle   water <NA>        0.5       9             45    44     48      65
 8 Wartortle  water <NA>        1        22.5           45    59     63      80
 9 Blastoise  water <NA>        1.6      85.5           45    79    103     120
10 Caterpie   bug   <NA>        0.3       2.9          255    45     30      35
# ℹ 791 more rows
# ℹ 5 more variables: sp_attack <dbl>, sp_defense <dbl>, speed <dbl>,
#   generation <dbl>, is_legendary <dbl>

Counting categories

We can use a new function count(), to count how many observations are in each category:

pokemon %>% 
  count(type1)

# A tibble: 18 × 2
   type1        n
   <chr>    <int>
 1 bug         72
 2 dark        29
 3 dragon      27
 4 electric    39
 5 fairy       18
 6 fighting    28
 7 fire        52
 8 flying       3
 9 ghost       27
10 grass       78
11 ground      32
12 ice         23
13 normal     105
14 poison      32
15 psychic     53
16 rock        45
17 steel       24
18 water      114

From counts to percents

We can can then use mutate() to calculate the percent in each group:

pokemon %>% 
  count(type1) %>% 
  mutate(percent = n / sum(n) * 100)

# A tibble: 18 × 3
   type1        n percent
   <chr>    <int>   <dbl>
 1 bug         72   8.99 
 2 dark        29   3.62 
 3 dragon      27   3.37 
 4 electric    39   4.87 
 5 fairy       18   2.25 
 6 fighting    28   3.50 
 7 fire        52   6.49 
 8 flying       3   0.375
 9 ghost       27   3.37 
10 grass       78   9.74 
11 ground      32   4.00 
12 ice         23   2.87 
13 normal     105  13.1  
14 poison      32   4.00 
15 psychic     53   6.62 
16 rock        45   5.62 
17 steel       24   3.00 
18 water      114  14.2

Don’t forget!

We can then store as object for plotting:

type_pct = pokemon %>% 
  count(type1) %>% 
  mutate(percent = n/sum(n) * 100)

The plot

Code

ggplot(type_pct, aes(y = reorder(type1, percent), 
                     x = percent)) + 
  geom_col(color = "white", fill = "darkblue") + 
  theme(legend.position = "none") +
  labs(x = "Percent of Pokemon", 
       y = "Type", 
       title = "Distribution of Pokemon types")

🚨 Your turn: 💺 Flying etiquette 💺 🚨

A survey of what’s rude to do on a plane:

Sample from the flying dataset
gender	age	height	children_under_18	household_income	education	location	frequency	recline_frequency	recline_obligation	recline_rude	recline_eliminate	switch_seats_friends	switch_seats_family	wake_up_bathroom	wake_up_walk	baby	unruly_child	two_arm_rests	middle_arm_rest	shade	unsold_seat	talk_stranger	get_up	electronics	smoked
Male	45-60	6'5"	TRUE	$50,000 - $99,999	Bachelor degree	South Atlantic	A few times per week	Always	FALSE	No	FALSE	No	No	No	No	No	No	Other (please specify)	Other (please specify)	Everyone in the row should have some say	No	No	More than five times times	TRUE	TRUE
Female	30-44	5'4"	FALSE	$25,000 - $49,999	Some college or Associate degree	Pacific	Once a year or less	Always	FALSE	No	FALSE	Somewhat	Somewhat	No	Somewhat	No	Very	The person in the middle seat gets both arm rests	The arm rests should be shared	The person in the window seat should have exclusive control	Very	Somewhat	Once	FALSE	FALSE
Male	> 60	6'0"	FALSE	$50,000 - $99,999	Bachelor degree	West South Central	Once a year or less	Usually	TRUE	No	FALSE	No	No	No	No	No	Somewhat	The arm rests should be shared	The arm rests should be shared	The person in the window seat should have exclusive control	No	No	Three times	FALSE	FALSE
Female	> 60	5'3"	FALSE	NA	Some college or Associate degree	West South Central	Once a month or less	About half the time	FALSE	No	FALSE	Somewhat	No	No	No	No	Somewhat	The arm rests should be shared	The arm rests should be shared	The person in the window seat should have exclusive control	No	No	Three times	TRUE	FALSE
Female	> 60	5'5"	FALSE	NA	Less than high school degree	West North Central	Once a year or less	Usually	TRUE	No	FALSE	No	No	Somewhat	Very	No	Very	Whoever puts their arm on the arm rest first	Whoever puts their arm on the arm rest first	Everyone in the row should have some say	No	No	Three times	TRUE	FALSE
Female	> 60	5'6"	FALSE	$25,000 - $49,999	High school degree	New England	Once a year or less	About half the time	TRUE	Somewhat	FALSE	No	No	Somewhat	Somewhat	No	No	The arm rests should be shared	The arm rests should be shared	The person in the window seat should have exclusive control	Somewhat	No	Three times	FALSE	FALSE
Male	30-44	5'7"	TRUE	$50,000 - $99,999	Bachelor degree	South Atlantic	Once a year or less	Once in a while	FALSE	No	FALSE	No	No	Somewhat	Very	No	Very	The arm rests should be shared	The arm rests should be shared	Everyone in the row should have some say	Somewhat	No	Twice	FALSE	FALSE
Male	18-29	5'2"	FALSE	$50,000 - $99,999	Bachelor degree	West South Central	Once a year or less	Once in a while	FALSE	Somewhat	FALSE	Somewhat	No	Very	Very	Somewhat	Somewhat	The arm rests should be shared	The arm rests should be shared	The person in the window seat should have exclusive control	No	No	Twice	FALSE	FALSE
Male	30-44	5'6"	FALSE	$50,000 - $99,999	Bachelor degree	West South Central	Once a month or less	About half the time	FALSE	No	FALSE	Somewhat	Somewhat	Somewhat	Somewhat	Somewhat	Very	The arm rests should be shared	The arm rests should be shared	Everyone in the row should have some say	Somewhat	No	Twice	FALSE	FALSE
Female	18-29	5'7"	FALSE	$0 - $24,999	Bachelor degree	East South Central	Once a year or less	Never	TRUE	Somewhat	TRUE	No	No	Somewhat	Very	No	Very	The arm rests should be shared	The arm rests should be shared	The person in the window seat should have exclusive control	No	No	Twice	FALSE	FALSE

🚨 Your turn: 💺 flying etiquette 💺 🚨

Using the flying data from fivethirtyeight

In a row of three seats, who should get to use the middle arm rest (two_arm_rests)? Make a barplot of the percent of respondents who gave each answer.
In general, is it rude to knowingly bring unruly children on a plane? Make a barplot of the percent who gave each answer, but separated by whether the respondent has a kid or not.
Make a barplot of responses to an etiquette dilemma of your liking. Bonus points if you break it down by a respondent characteristic.

15:00